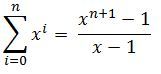Matematika - řada

To jde různě, samozřejmě pokud x je různé od jedné.

Takový přímočarý způsob je matematická indukce. Pro n = 0 je to triviální rovnost 1 = 1; pokud chcete, můžete do zkusit ještě pro n = 1, pak je to vzorec pro rozdíl čtverců (uvědomte si, že 1² = 1 ). No a indukční krok je snadný: předpokládám, že vzorec platí pro nějaké n. Následně k oběma stranám přičtu x^(n+1) a snadnými úpravami pravé strany dostanu tentýž vzorec, ale pro n o jedna větší.

Nebo to mohu zkusit přímo, začnu tak, že vzorec roznásobím x-1. Napravo mi zůstane x^(n+1)-1, levou stranu si raději rozepíšu bez sumačního znaménka, jde to i bez toho, ale takhle to bude názornější.

Nalevo budete mít po odstraněí sumítka konečnou geometrickou řadu

x^n + x^(n-1)+...+1

(napsal jsem ji od konce) . Když ji vynásobíte x, tak se vám prostě "posune doleva" a budete mít řadu

x^(n+1) +x^n + ... + x

No a teď tu původní řadu vynásobím -1 (neboli změním znaménka) a napíšu ji pod tu posunutou, ale "neposunutě", tak. že pod x^(n+1) nebude nic, pod x^n bude -x^n atd, až pod x bude -x a pod volným místem bude -1. Podtrženo sečteno se nám ty odpovídající mocniny počínaje n-tou a konče první zruší a zbydou jen ty kraje, to jest kýžené x^(n+1)-1

V podstatě se jedná o součet prvních n členů geometrické posloupnosti:
s_n = a₁ (qⁿ– 1)/(q – 1) ... q je různé1
První člen vaší posloupnosti je x⁰ = 1, kvocient je x, n-tý člen je x^n-1. Členů je n + 1 a jejich součet je tudíž

(xⁿ⁺¹– 1)/(x – 1) ... x je různé 1