Nejste přihlášen/a.
Dokázal by mi někdo pomoct s těmito rovnicemi? Potřeboval bych znát postup :-/
(x-3)*(x-4)+x2=3x-2-5
3x-2y/5 + 5x-3y/3=x+1
x+2y-3z=-8

1x
2 x2 - 10 x + 19 = 0 a jejím řešením je x1,2 = ½ (5 ± i√13)
Postup řešení ukážu na poslední rovnici 5x2 _ 18x _ 8 = 0
Nejprve vypočteme diskriminant:
a = 5
b = -18
c = - 8___
D = b2 − 4ac = (-18)2 _ 4⋅5⋅(-8) = 484 => rovnice bude mít dva reálné kořeny
doplněno 21.12.11 12:31:
U druhého kořenu má být index 2 → x2
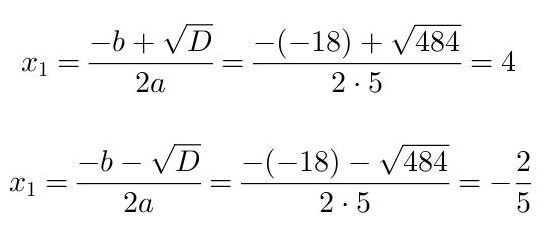
1x
Příklad 3:
x + 2y – 3z = -8
-3x + y + 2z = 102x – 3y + 2z = 5_
První rovnici vynásobíme 2 a poslední 3 a rovnice sečteme
2x + 4y – 6z = -16
6x – 9y + 6z = 15_
8x – 5y = -1
Od druhé rovnice odečteme třetí
-3x + y + 2z = 10
2x – 3y + 2z = 5_
-5x + 4y = 5
Nyní již máme soustavu dvou rovnic o dvou neznámých
8x – 5y = -1
-5x + 4y = 5
Zde vynásobíme první rovnici 4 a druhou 5
32x – 20y = -4
-25x + 20y = 25
a rovnice sečteme
7x = 21 =>x = 3
Nyní za x dosadíme např. do rovnice -5x + 4y = 5
-5⋅ 3 + 4y = 5 =>y = 5
a nakonec dosadíme za x a y např. do rovnice 2x – 3y + 2z = 5
2⋅3 – 3⋅5 + 2z = 5 =>z = 7
Řešení je tedy x = 3; y = 5; z = 7.
0x
Tak rovnice o 1 neznámé, tam si roznásobíš závorky a pak uvidíš co ti vznikne, pravděpodobně kvadratická rovnice...
Rovnice o 2 neznámých - z jedné rovnice si osamostatníš např. x a dosadíš do druhé rovnice. Spočítáš ji stejným způsobem jako rovnici s 1 neznámou a poté dopočítáš x.
No a s 3 - postup stejný jako u 2 - akorát že si z jedné osamostatníš x, pak ti dosadíš do druhé, z té si osamostatníš y a dosadíš do poslední. Pak jenom dopočítáš x a y.
0x
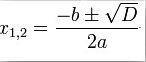
0x
Kdyby jste měl zájem mohu naskenované řešení poslat na mail .. ![]() )
)
Ale samozdřejmě nejlepším je si to spočítat sám ![]() )Nejlépší pro pochopení :D
)Nejlépší pro pochopení :D
0x
Abychom odstranili zlomky, vynásobíme první rovnici 15 a druhou 3
3(3x _ 2y) + 5(5x _ 3y) = 15(x + 1)
2x + 3y + 4x _ 3y = 3y___________
Roznásobíme a upravíme
19x _ 21y = 15
__6x _ 9y = 0_
Druhou rovnici vydělíme 3
19x _ 21y = 15
__2x _ 3y = 0_
Nyní druhou rovnici vynásobíme -7
19x _ 21y = 15
-14x + 21y = 0_
a rovnice sečteme
19x _ 14x = 15 => x = 3
Za x dosadíme do rovnice 2x _ 3y = 0
2⋅3 _ 3y = 0 => y = 2
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.
