Dobrý den,
chtěl bych se zeptat na vztahy koeficientů a kořenů kvadr. rovnice. Tedy spíše mi jde o to, abych napsal program(ve Visual Basicu) s algoritmem: Uživatel zadá interval(např. <-5;10>) ze kterého budou kořeny x1 a x2 -> program vyhodí možná řešení koeficintů (a= .., b=.., c=...). Vše ostatní bych napsal uměl, ale nevím vzorec, jak dostat z x1 a x2 ty koeficinty(aniž bych znal cokoliv jiného).
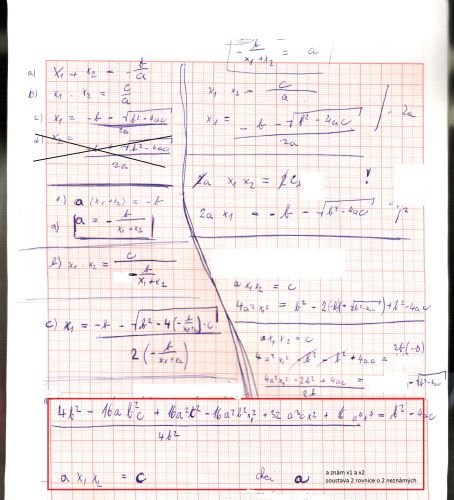
Na obr. přidávám svůj postup, jak jsem chtěl z rovnice které znám -> udělat soustavu 3 rovnic o 3 neznámých (znám x1, x2 a neznám a, b, c) - ( v červeném obdelníku je mnou ta soustava upravená jen na 2 neznámé a 2 rovnice, ale bohužel pak nevím už jak dál![]() )
)
Můžete někdo prosím poradit ![]()
Je to takto vůbec možné?
Za každý nápad nebo radu budu rád.
Předem děkuji
Lukáš B.
doplněno 13.12.11 11:59: Zde je radši ještě link na stažní ukázaného obr.(není nejlépe vidět)
leteckaposta.cz/...
3x
To nemáte jednoznačně určeno. Pro každé x1,x2 existuje nekonečně mnoho kvadratických rovnic, které jsou jimi řešeny. x^2=4, -2x^2=-8, (x^2)/2=1 atd, určitě chápete. Máte prostě na ose x dva body, které má parabola protnout, jenže takovejch si můžete namalovat spoustu (různé "otevření").
Dalo by se to omezit třeba tak, že by v zadání bylo a=1, tj "standardní" parabola. Pak vám jedna rovnice vypadne a snadno to spočítáte. Ze vzorce pro x1,x2 vlastně budete mít x1=[-b+√(b^2-4c)]/2, x2=[-b-√(b^2-4c)]/2, x máte zadané, takže dvě rovnice s neznámými b, c.
Ano děkuji,
jen jsem myslel jestli to nelze vyjádřit nějak obecně ...
Jak říkáte pro každé x1 a x2 je nekonečně mnoho řešení tudíž tedy jestli se nedají nějak vypočítat...
Jinak to teda udělám tak, že za "a" dám 1 a bude.. Uživatel si bude moci "a" změnit.
Ještě jednou díky
Je mi jedno jaké z těch nekonečně mnoho řešení ten program vypíše.
2x
Obrázek jaksi nevidím, ale co se týká vztahu mezi kořeny a koeficienty, ten je jednoduchý. Pro rovnici tvaru x2 + px + q = 0 platí
x1 + x2 = – p, x1*x2 = q. Pro rovnici ax2 +bx +c = 0 (pro obecné nenulové a) vztah dostanete, když rovnici tím a vydělíte. Může mít tedy tvar
x1 + x2 = – b/a, x1*x2 = c/a, nebo ho múžete tím a vynásobit, pokud by to tak lépe vhovovlo k dalším úpravám. (Zjistíte to z kořenového tvaru rovnice a platí to i pro komplexní kořeny.)
doplněno 13.12.11 12:23:Tak teď už tam ten obrázek je a vidím, že základní vzorec znáte. V tom tedy bla má rada zbytečná, důležité pro vás je spíš to, co píše dzordz, tedy že bez dalšího omezní koeficienty a, b, c jednoznačně neurčíte.
doplněno 13.12.11 12:39:V tom červeném rámečku áte pořád tři neznámé a, b, c. Prostě řešení je jednoznačné až na multiplikativní konstantu.
Omlouvám, že píši až nyní, ale nebyl jsem v ČR.
Mám ještě problém( u toho když položím že a = 1, tak mám 2 rovnice s 2 nenámými(x1,2 znám to ano, ale po úpravě by vychází toho:
{b2 -> Sqrt[ 1 - 2 c + 2 x^2 - Sqrt[1 - 8 c + 4 x^2]]},
{b3 -> -Sqrt[ 1 - 2 c + 2 x^2 + Sqrt[1 - 8 c + 4 x^2]]},
{b4 -> Sqrt[ 1 - 2 c + 2 x^2 + Sqrt[1 - 8 c + 4 x^2]]}}
To je OK.
Nyní b dosadím do x2=( -b+Sqrt(D))/2:
((-1*-Sqrt[1 - 2 c + 2 x^2 - Sqrt[1 - 8 c + 4 x^2]]) + Sqrt[1 - 2 c + 2 x^2 - Sqrt[1 - 8 c + 4 x^2] - 4*c])/2 == w
Kde w=x2
a z této rovnice si vyjádřím c. A zde nastává problém Vyjádření c vypadá takto:
c1 -> -2 w^2 -
1/2 [Sqrt](16 w^4 -
4/3 w^2 (-1 + 9 w^2 - 2 x^2) + (4 2^(
1/3) (w^4 - 24 w^6 + 36 w^8 + 4 w^4 x^2 + 48 w^6 x^2 +
16 w^4 x^4))/(3 (-16 w^6 + 144 w^8 - 3456 w^10 +
3456 w^12 - 96 w^6 x^2 - 1728 w^8 x^2 + 6912 w^10 x^2 +
384 w^6 x^4 + 4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 - 27648 w^12 x^4 +
884736 w^14 x^4 - 2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3)) +
1/(3 2^(1/3))((-16 w^6 + 144 w^8 - 3456 w^10 + 3456 w^12 -
96 w^6 x^2 - 1728 w^8 x^2 + 6912 w^10 x^2 + 384 w^6 x^4 +
4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 - 27648 w^12 x^4 +
884736 w^14 x^4 - 2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3)) -
1/2 [Sqrt](32 w^4 -
8/3 w^2 (-1 + 9 w^2 - 2 x^2) - (4 2^(
1/3) (w^4 - 24 w^6 + 36 w^8 + 4 w^4 x^2 + 48 w^6 x^2 +
16 w^4 x^4))/(3 (-16 w^6 + 144 w^8 - 3456 w^10 +
3456 w^12 - 96 w^6 x^2 - 1728 w^8 x^2 + 6912 w^10 x^2 +
384 w^6 x^4 + 4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 - 27648 w^12 x^4 +
884736 w^14 x^4 - 2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3)) -
1/(3 2^(1/3))((-16 w^6 + 144 w^8 - 3456 w^10 + 3456 w^12 -
96 w^6 x^2 - 1728 w^8 x^2 + 6912 w^10 x^2 + 384 w^6 x^4 +
4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 - 27648 w^12 x^4 +
884736 w^14 x^4 - 2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(
1/3)) - (-512 w^6 - 64 w^4 (w^2 - 2 x^2) +
64 w^4 (-1 + 9 w^2 - 2 x^2))/(4 [Sqrt](16 w^4 -
4/3 w^2 (-1 + 9 w^2 - 2 x^2) + (4 2^(
1/3) (w^4 - 24 w^6 + 36 w^8 + 4 w^4 x^2 +
48 w^6 x^2 + 16 w^4 x^4))/(3 (-16 w^6 + 144 w^8 -
3456 w^10 + 3456 w^12 - 96 w^6 x^2 - 1728 w^8 x^2 +
6912 w^10 x^2 + 384 w^6 x^4 + 4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 -
27648 w^12 x^4 + 884736 w^14 x^4 -
2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3)) +
1/(3 2^(1/3))((-16 w^6 + 144 w^8 - 3456 w^10 +
3456 w^12 - 96 w^6 x^2 - 1728 w^8 x^2 +
6912 w^10 x^2 + 384 w^6 x^4 + 4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 -
27648 w^12 x^4 + 884736 w^14 x^4 -
2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3))}
c2-> -2 w^2 -
1/2 [Sqrt](16 w^4 -
4/3 w^2 (-1 + 9 w^2 - 2 x^2) + (4 2^(
1/3) (w^4 - 24 w^6 + 36 w^8 + 4 w^4 x^2 + 48 w^6 x^2 +
16 w^4 x^4))/(3 (-16 w^6 + 144 w^8 - 3456 w^10 +
3456 w^12 - 96 w^6 x^2 - 1728 w^8 x^2 + 6912 w^10 x^2 +
384 w^6 x^4 + 4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 - 27648 w^12 x^4 +
884736 w^14 x^4 - 2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3)) +
1/(3 2^(1/3))((-16 w^6 + 144 w^8 - 3456 w^10 + 3456 w^12 -
96 w^6 x^2 - 1728 w^8 x^2 + 6912 w^10 x^2 + 384 w^6 x^4 +
4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 - 27648 w^12 x^4 +
884736 w^14 x^4 - 2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3)) +
1/2 [Sqrt](32 w^4 -
8/3 w^2 (-1 + 9 w^2 - 2 x^2) - (4 2^(
1/3) (w^4 - 24 w^6 + 36 w^8 + 4 w^4 x^2 + 48 w^6 x^2 +
16 w^4 x^4))/(3 (-16 w^6 + 144 w^8 - 3456 w^10 +
3456 w^12 - 96 w^6 x^2 - 1728 w^8 x^2 + 6912 w^10 x^2 +
384 w^6 x^4 + 4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 - 27648 w^12 x^4 +
884736 w^14 x^4 - 2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3)) -
1/(3 2^(1/3))((-16 w^6 + 144 w^8 - 3456 w^10 + 3456 w^12 -
96 w^6 x^2 - 1728 w^8 x^2 + 6912 w^10 x^2 + 384 w^6 x^4 +
4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 - 27648 w^12 x^4 +
884736 w^14 x^4 - 2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(
1/3)) - (-512 w^6 - 64 w^4 (w^2 - 2 x^2) +
64 w^4 (-1 + 9 w^2 - 2 x^2))/(4 [Sqrt](16 w^4 -
4/3 w^2 (-1 + 9 w^2 - 2 x^2) + (4 2^(
1/3) (w^4 - 24 w^6 + 36 w^8 + 4 w^4 x^2 +
48 w^6 x^2 + 16 w^4 x^4))/(3 (-16 w^6 + 144 w^8 -
3456 w^10 + 3456 w^12 - 96 w^6 x^2 - 1728 w^8 x^2 +
6912 w^10 x^2 + 384 w^6 x^4 + 4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 -
27648 w^12 x^4 + 884736 w^14 x^4 -
2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3)) +
1/(3 2^(1/3))((-16 w^6 + 144 w^8 - 3456 w^10 +
3456 w^12 - 96 w^6 x^2 - 1728 w^8 x^2 +
6912 w^10 x^2 + 384 w^6 x^4 + 4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 -
27648 w^12 x^4 + 884736 w^14 x^4 -
2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(
1/3))}, {c -> -2 w^2 +
1/2 [Sqrt](16 w^4 -
4/3 w^2 (-1 + 9 w^2 - 2 x^2) + (4 2^(
1/3) (w^4 - 24 w^6 + 36 w^8 + 4 w^4 x^2 + 48 w^6 x^2 +
16 w^4 x^4))/(3 (-16 w^6 + 144 w^8 - 3456 w^10 +
3456 w^12 - 96 w^6 x^2 - 1728 w^8 x^2 + 6912 w^10 x^2 +
384 w^6 x^4 + 4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 - 27648 w^12 x^4 +
884736 w^14 x^4 - 2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3)) +
1/(3 2^(1/3))((-16 w^6 + 144 w^8 - 3456 w^10 + 3456 w^12 -
96 w^6 x^2 - 1728 w^8 x^2 + 6912 w^10 x^2 + 384 w^6 x^4 +
4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 - 27648 w^12 x^4 +
884736 w^14 x^4 - 2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3)) -
1/2 [Sqrt](32 w^4 -
8/3 w^2 (-1 + 9 w^2 - 2 x^2) - (4 2^(
1/3) (w^4 - 24 w^6 + 36 w^8 + 4 w^4 x^2 + 48 w^6 x^2 +
16 w^4 x^4))/(3 (-16 w^6 + 144 w^8 - 3456 w^10 +
3456 w^12 - 96 w^6 x^2 - 1728 w^8 x^2 + 6912 w^10 x^2 +
384 w^6 x^4 + 4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 - 27648 w^12 x^4 +
884736 w^14 x^4 - 2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3)) -
1/(3 2^(1/3))((-16 w^6 + 144 w^8 - 3456 w^10 + 3456 w^12 -
96 w^6 x^2 - 1728 w^8 x^2 + 6912 w^10 x^2 + 384 w^6 x^4 +
4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 - 27648 w^12 x^4 +
884736 w^14 x^4 - 2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(
1/3)) + (-512 w^6 - 64 w^4 (w^2 - 2 x^2) +
64 w^4 (-1 + 9 w^2 - 2 x^2))/(4 [Sqrt](16 w^4 -
4/3 w^2 (-1 + 9 w^2 - 2 x^2) + (4 2^(
1/3) (w^4 - 24 w^6 + 36 w^8 + 4 w^4 x^2 +
48 w^6 x^2 + 16 w^4 x^4))/(3 (-16 w^6 + 144 w^8 -
3456 w^10 + 3456 w^12 - 96 w^6 x^2 - 1728 w^8 x^2 +
6912 w^10 x^2 + 384 w^6 x^4 + 4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 -
27648 w^12 x^4 + 884736 w^14 x^4 -
2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3)) +
1/(3 2^(1/3))((-16 w^6 + 144 w^8 - 3456 w^10 +
3456 w^12 - 96 w^6 x^2 - 1728 w^8 x^2 +
6912 w^10 x^2 + 384 w^6 x^4 + 4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 -
27648 w^12 x^4 + 884736 w^14 x^4 -
2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(
1/3))}, {c -> -2 w^2 +
1/2 [Sqrt](16 w^4 -
4/3 w^2 (-1 + 9 w^2 - 2 x^2) + (4 2^(
1/3) (w^4 - 24 w^6 + 36 w^8 + 4 w^4 x^2 + 48 w^6 x^2 +
16 w^4 x^4))/(3 (-16 w^6 + 144 w^8 - 3456 w^10 +
3456 w^12 - 96 w^6 x^2 - 1728 w^8 x^2 + 6912 w^10 x^2 +
384 w^6 x^4 + 4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 - 27648 w^12 x^4 +
884736 w^14 x^4 - 2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3)) +
1/(3 2^(1/3))((-16 w^6 + 144 w^8 - 3456 w^10 + 3456 w^12 -
96 w^6 x^2 - 1728 w^8 x^2 + 6912 w^10 x^2 + 384 w^6 x^4 +
4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 - 27648 w^12 x^4 +
884736 w^14 x^4 - 2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3)) +
1/2 [Sqrt](32 w^4 -
8/3 w^2 (-1 + 9 w^2 - 2 x^2) - (4 2^(
1/3) (w^4 - 24 w^6 + 36 w^8 + 4 w^4 x^2 + 48 w^6 x^2 +
16 w^4 x^4))/(3 (-16 w^6 + 144 w^8 - 3456 w^10 +
3456 w^12 - 96 w^6 x^2 - 1728 w^8 x^2 + 6912 w^10 x^2 +
384 w^6 x^4 + 4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 - 27648 w^12 x^4 +
884736 w^14 x^4 - 2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3)) -
1/(3 2^(1/3))((-16 w^6 + 144 w^8 - 3456 w^10 + 3456 w^12 -
96 w^6 x^2 - 1728 w^8 x^2 + 6912 w^10 x^2 + 384 w^6 x^4 +
4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 - 27648 w^12 x^4 +
884736 w^14 x^4 - 2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(
1/3)) + (-512 w^6 - 64 w^4 (w^2 - 2 x^2) +
64 w^4 (-1 + 9 w^2 - 2 x^2))/(4 [Sqrt](16 w^4 -
4/3 w^2 (-1 + 9 w^2 - 2 x^2) + (4 2^(
1/3) (w^4 - 24 w^6 + 36 w^8 + 4 w^4 x^2 +
48 w^6 x^2 + 16 w^4 x^4))/(3 (-16 w^6 + 144 w^8 -
3456 w^10 + 3456 w^12 - 96 w^6 x^2 - 1728 w^8 x^2 +
6912 w^10 x^2 + 384 w^6 x^4 + 4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 -
27648 w^12 x^4 + 884736 w^14 x^4 -
2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3)) +
1/(3 2^(1/3))((-16 w^6 + 144 w^8 - 3456 w^10 +
3456 w^12 - 96 w^6 x^2 - 1728 w^8 x^2 +
6912 w^10 x^2 + 384 w^6 x^4 + 4608 w^8 x^4 +
1024 w^6 x^6 + [Sqrt](13824 w^14 - 338688 w^16 +
3760128 w^18 - 3981312 w^20 + 138240 w^14 x^2 -
276480 w^16 x^2 - 5308416 w^18 x^2 -
27648 w^12 x^4 + 884736 w^14 x^4 -
2764800 w^16 x^4 - 221184 w^12 x^6 -
1327104 w^14 x^6 - 442368 w^12 x^8))^(1/3))
A takto vyjádřené c zas dosazovat zpátky do předchozích rovnic je skoro nemožné pak v programu. Je toto opravdu jediné řešení?
Děkuji za pomoc
Výsledky jsou určitě správně - vypočítáno pomocí Wolfram Mathematica 8.0
Proč takhle strašně složitě? Však to spočítejte z těch Kartagincových rovnic s koeficienty.
Nebo když už to chcete počítat z těch dvou, co jsem psal, tak to upravte jinak:
Soustava x1=[-b+√(b^2-4c)]/2, x2=[-b-√(b^2-4c)]/2
upravím na √(b^2 - 4c) = 2x1 + b, √(b^2 - 4c)= -2x2 - b, levé strany jsou stejné, pravé se musejí rovnat, tedy 2x1 + b = -2x2 - b, po úpravě x1 + x2 = -b (tj přesně ta koeficientová rovnice).
Dosadíte zpátky, c = [b^2 - (2x1 + b)^2] / 4, upraví se postupně na c = [b^2 - (2x1 + b)^2] / 4, c = (-4x1^2 - 4x1 * b) / 4, c = -x1^2 - x1 * (-x1 - x2), což je překvapivě ta druhá rovnice, c = x1 * x2 ![]()
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.