Nejste přihlášen/a.
dobrý den, mám dotaz, jak spolu souvisí derivace a limita?stejné to není, že?zrovna se to učím a jsem z toho zmatena,
doplněno 11.12.11 13:23:prosím vysvětlete mě to ať to pochopí a takový blbec, jak jsem já![]() díky
díky
4x
Zjednodušeně: limita je hodnota, ke které se něco (hodnota funkce, hodnota posloupnosti) neomezeně blíží (například lim (1/x) = + nekonečno, pokud se x blíží k nule kladnými hdnotami; zde ovšem jde o tzv. "nevlastní limitu" a neříkáme, že 1/x se blíží k nekonečnu, ale že roste nade všechny meze); nebo lim (sin x) = 0, když x se blíží k nule, podobně lim (sin x)/x = 1 při x jdoucím k nule (formální zápis je takový, že to x jdouci k nule se zapíše pod zkratku lim pomocí šipky, asi takto x->0)
Derivace je pak limita zcela speciálního výrazu. Příklad: průměrnou rychlost zapíšeme jako podíl dráhy (uražené v nějakém česovém úseku t ) a právě toho t. Když pak necháme t blížiti se k nule, vyjde nám (možná) nějaká limita, ve fyzice jí říkáme okamžitá rychlost, z matematického hlediska je to derivace dráhy podle času.
3x
Tady je to po lopatě vysvětlené:
Matematika polopatě— pro základní, střední a vysoké školy
doplněno 11.12.11 14:55:
Tady je to dostatečně vysvětlené, to je jen kousek z Google
Derivace je základní pojem v diferenciálním počtu, má významnou roli například při určování průběhu funkce a je na jedné straně nenáviděna studenty a na druhou stranu derivaci spočítá i patřičně cvičená opice. V tomto článku bude pouze popsána a vysvětlena definice derivace a související pojmy. Řešené příklady naleznete v sousedních článcích: jednoduché příklady naderivace a složitější příklady.
Co je to derivace
Než se vůbec dostaneme k definici derivace, řekneme si, co vůbec derivací spočítáme a k čemu nám to následně může být dobré.
Derivací funkce získáme směrnici tečny. To je asi hodně sprostých slov pohromadě, takže od začátku. Jednoduše řečeno, tečna je přímka, která se daného grafu dotýká právě v jednom bodě. Přesná definice to není, tu si přečtěte třeba naWikipedii, ale zhruba stačí. Nyní si prohlédněte následující obrázek:
Černá křivka je graf funkcey = x2. Modrá přímka je tečna k této funkci v boděD =[1, 1], označen červeně. Zeleně je vyznačen úhel α, který svírá tečna s osoux— přesněji s kladnou poloosoux. Nyní si definujeme pojem směrnice tečny. Směrnice tečny je v tomto obrázkutangensúhlu alfa. Tangens je klasická goniometrická funkce, díky které můžeme například počítat úhly a velikosti stran vtrojúhelníku. Takže směrnice tečny je tangens úhlu, který daná tečna svírá s kladnou poloosoux. A tuto směrnici získáme právě pomocí derivací.
Dále rozlišujeme pojmy derivace funkce v bodě a derivace funkce. Derivace funkce v bodě představuje právě směrnici tečny v daném bodě. Derivace funkce je pak jiná funkce, která předepisuje směrnice pro obecný argumentx. Příklad následuje.
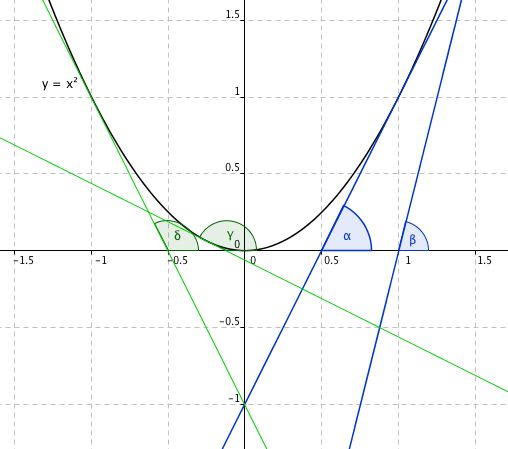
Pomocí derivace tak umíme spočítat směrnice tečen. K čemu to může být dobré? Prohlédněte si následující obrázek:
Na obrázku je opět funkcey = x2a čtyři vyznačené tečny. Dvě zelené a dvě modré. Všimněte si, že funkcey = x2je na intervalu(−∞, 0)klesající, zatímco na intervalu(0, &infin![]() je rostoucí. Co ale zároveň platí pro jejich tečny, respektive pro úhel, který svírají s kladnou poloosou? Modré tečny, což jsou tečny, která prochází body, které přísluší intervalu, ve kterém funkce roste, svírají s osou úhel menší než 90 stupňů. Zatímco zelené tečny svírají s osou úhel, který je větší než 90 stupňů. Jak se to projeví do směrnic tečen?
je rostoucí. Co ale zároveň platí pro jejich tečny, respektive pro úhel, který svírají s kladnou poloosou? Modré tečny, což jsou tečny, která prochází body, které přísluší intervalu, ve kterém funkce roste, svírají s osou úhel menší než 90 stupňů. Zatímco zelené tečny svírají s osou úhel, který je větší než 90 stupňů. Jak se to projeví do směrnic tečen?
K tomu potřebujeme znát chování funkce tangens. Z následující grafu se dovíme, že pokud má úhel velikost menší než 90 stupňů, pak je hodnota tangensu kladná (modře zvýrazněná část); naopak pokud je úhel větší než 90 stupňů, ale menší než 180 stupňů (tj. menší než Pí radiánů), pak je hodnota tangensu záporná. Jaký tak můžeme učinit závěr? Pokud je směrnice (nezapomeňte, že směrnice je právě tangens úhlu) tečny v daném bodě kladná, pak je funkce v daném bodě rostoucí, pokud je záporná, pak je klesající.
Obrázky jsou v Google- Matematika po lopatě, jak je nahoře psaný odkaz
1x
Jedna z definic derivace zní následovně (existují asi 3 různé): Funkce f má derivaci v bodě a, pokud existuje limita lim (x->a) z podílu f(x) - f(a) / (x - a). Derivace je vlastní, pokud je výsledek limity reálné číslo. Jinak je nevlastní. Z této limity se také odvozují známé "vzorečky" pro derivaci různých funkcí, ale také například součinu (podílu) funkcí a derivace složené funkce. Tudíž pokud derivujete funkci, tak je to totéž, jako řešit limitu funkce v obecném bodě definičního oboru.
Například derivace sin(x):
lim (x->a) (sin(x) - sin(a) ) / (x-a) = cos(a)
nebo derivace ln(x)
lim (x->a) (ln(x) - ln(a) ) / (x-a) = 1/a
což odpovídá zmíněným "vzorečkům" pro derivaci elementární funkce.
1x
defivace funkce vlastně vyjadřuje v jejím místě (x) změnu této funkce k nekonečně malé změně jejích argumentů tj. diference X se blíží nule. Zkusme to napříkladu klasické paraboly Y=x^2 je deroivováno y=2X, což vyjadřuje v každém místě původní funkce směrnici tečny v místě X. Musím podotkout že vikipedie to popisuje celkem přesně.
Limita je něco jiného = hodnota funkce. Defivace je vlastně něco jako hodnota nejmenšího přírůstku. Snad jsem Vás nezmátl.
0x
Úplně jednoduše. Derivace znamená něco, co je odvozeno od nějakého daného základu. Limita je od slova "limit", tudíž něco, co co nejde dál rozvíjet. Jsem blbec, a odpověděla jsem také podle toho. Ale je to jednoduché. Tyto dva výrazy spolu samozřejmě nikterak nesouvisí. A proč tomu tak není, tak na to Ti odpověděli vzdělanější rádci. Já jenom tak pro jednoduchou obraznost, ze které pak můžeš vycházet při hlubším studiu. Snad Ti to pomůže. Je to jak sis přála, jednoduchými slovy. Jinak opravdu stačí zadat ty dva výrazy na Googlu a vyjede Ti tam všechno, od A až do Z. Ale je to dost komplikované a zašifrované ![]()
Výraz "derivát", se používá naprosto běžně u napodobenin světoznámých parfémů. Je to chemická "odvozenina" , za použití všelijakých náhražek. Raději už přestanu, nebo se do toho zase zamotám.
0x
Vysvětlené už to bylo, tak ti tu přidám 2 dobré stránky, které mně hodně v matice pomohly. user.mendelu.cz/... - tady máš teorii + názorné příklady propočítané krok za krokem, kromě limit a derivací tam jsou lokální extrémy, matice, ... wood.mendelu.cz/... - toto ti počítá příklady, dáš zadání a vyplivne ti to výsledek s postupem... jsou to supr věci, jenom je potřeba si to proklikat a zorientovat se v tom
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.