Nejste přihlášen/a.
Dobrý den,
mám vypočítat pár příkladů s vektory. Něco jsem vypočítal, ale nevím jestli dobře a něco mi moc nejde, pomůžete mi s tím prosím?
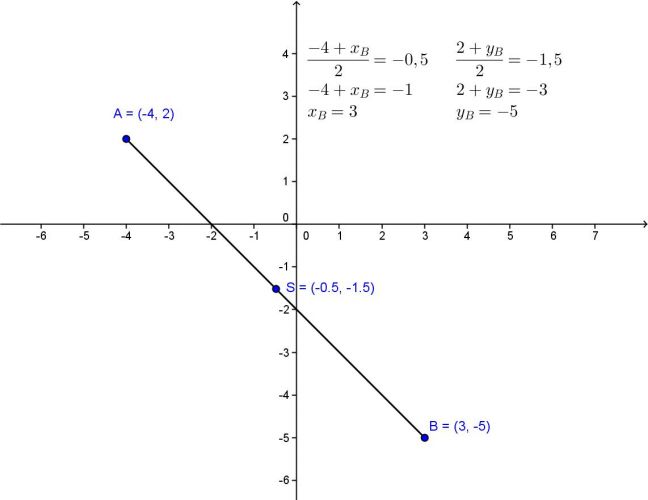
1) Je dán bod A a střed úsečky S. Určete souřadnice druhého bodu úsečky AB, je-li dáno: A = [ -4 ; 2] , B = [ -0,5 ; - 1.5]
Já jsem to počítal takto: |AS| = √(x2 _ x1)2 + (y2 _ y1)2 = √24,5 = 4,898
2) Určete neznámou souřadnici b2 tak, aby dané vektory byly kolineární : a = (7 ; -2) , b= (-2 ; b2)
Já jsem to počítal takto:
u1/v1= u2/v2
7/-2 = -2/7 násobit - 1
-7 / 2 = -7 / 2
- 3,5 = -3,5
3) Kolmost vektorů:
a) Určete, zda jsou vektory a = (- ¾ ; - 1) ; b = (4; 2) k sobě kolmé
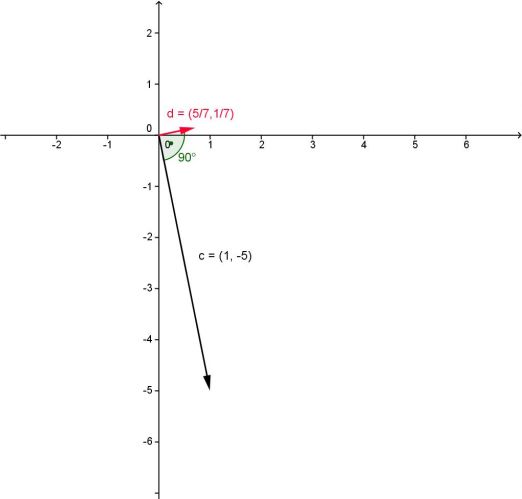
b) Určete neznámou souřadnici d2 tak, aby vektory c= (1; -5) ; d = (5/7 ; d2) byly na sebe kolmé.
4) Určete souřadnice směrového voktoru přímky, která je dána dvěma body. Ke směrovému vektoru určete vector normálový ( kolmý ke směrovému)
a) s = TU; T (2 ; 0); U (7; -2)
b) s = CD; C ( -2; 3,5); D (0; 5)
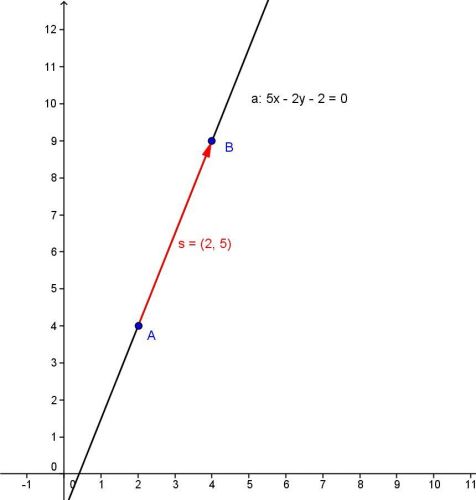
5) Napište parametrické rovnice přímky (parametrické vyjádření přímky), která prochází dvěma body: A ( 2 ; 4) ; B ( 4 ; 9)
6) Určete obecnou rovnici přímky q, která je dána bodem A = (3 ; 1) a směrovým vektorem s = (2 ; 3)
2x
s = (5; -2) → n = (2; 5) skalární součin (ne součet) je roven nule: s⋅n = 5⋅2 +(-2)⋅5 = 0
s = (2; 1,5) → n = (1,5; -2) skalární součin (ne součet) je roven nule: s⋅n = 2⋅1,5 +1,5⋅(-2) = 0
1x
Stačí vyřešit rovnice:
(-4 + xB)/2 = -0,5 => xB =
(2 + yB)/2 = -1,5 => yB =
2) Vektor b musí být násobkem vektoru a. Je patrné, že b1 = -2/7 ⋅ a1 Proto souřadnice b2 = -2 . -2/7 = 4/7
doplněno 07.12.11 17:07:
3)
a)Aby byly vektory kolmé, musí platit a1b1 + a2b2 = 0 a to neplatí, proto vektory nejsou vzájemně kolmé.b)Stačí vyřešit rovnici 1 ⋅ 5/7 + (-5) d2 = 0, kde neznámá je d2.
4) x souřadnici směrového vektoru vypočteme jako rozdíl x souřadnic bodů T, U, obdobně pak y souřadnici jako rozdíl y souřadnic bodů T, U.
Návod pro ty dva poslední příklady naleznete tady http://www.e-matematika.cz/stredni-skoly/jak-urcit-obecnou-rovnici-primky-urcene-dvema-body.php
nebo tady http://www.matweb.cz/primka
1x
s= (2; 3) =>n = (3; -2)
Rovnice přímky: 3x – 2y + c = 0
Dosadíme souřadnice bodu A a vypočteme c.
Ještě k tomu 5. příkladu. Přehlédl jsem, že se má napsat parametrické vyjádření přímky a nechal jsem se unést vaším nesprávným řešením. Parametrické vyjádření získáme pomocí směrového vektoru s = (2; 5) a jednoho bodu přímky, např. bodu A:
přímka a:
x = xA + ts1
y = yA + ts2
__________
x = 2 + 2t
y = 4 + 5t
1x
x = xM + ts1
y = yM + ts2
_______________
x = -1 _ t
y = 5 + 2t
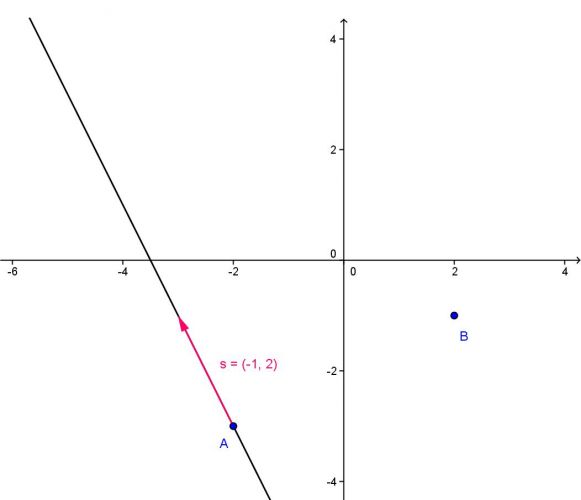
7b)
Parametrické rovnice přímky q určené bodem A a směrovým vektorem s= (-1; 2) jsou:
x = -2 _ t
y = -3 + 2t
Určíme hodnotu parametru t pro x souřadnici bodu B:
2 = -2 _ t => t = -4
Leží-li bod B na přímce q, pak i pro y souřadnici bodu B musí být stejná hodnota parametru t:
-1 = -3 + 2t => t = 1
Jelikož pro y souřadnici vychází jiná hodnota parametru t, bod B neleží na přímce q.
0x

a1, b1, c1, d1 jsou x souřadnice, a2, b2, c2, d2 jsou y souřadnice.
doplněno 16.12.11 13:43:
Obrázek
0x
Směrový vektor je určen body A, B: s= (4-2; 9-4) = (2; 5).
Normálový vektor pak bude n = (5; -2) ... prohodíme souřadnice a u jedné změníme znaménko.
Rovnice přímky je 5x -2y + c = 0
Jelikož bod A leží na přímce, musí jeho souřadnice vyhovovat rovnici přímky. Dosadíme jeho souřadnice do rovnice přímky a určíme hodnotu parametru c:
5⋅2 - 2⋅4 + c = 0 => c = -2
Rovnice přímky je 5x -2y -2 = 0
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.