Nejste přihlášen/a.
tab-stops:list 18.0pt" class="MsoNormal">1.V podstavě rovnostranného válce poloměru r je vedena tětiva délky r. Rovina proložená touto tětivou rovnoběžně s osou válce rozdělí na dvě úseče. Určete objempovrch větší z nich.
2.Dutá železná koule se ponoří do vody svou polovinou. Jaká je tloušťka její stěny, je-li vnější průměr koule 1 m a hustota železa je 7,8 g.cm-3?
3.urči poměr objemů rotačního válce ,polokoule a rotačního kužele se stejnými poloměry podstav a stejnými výškami.
4.jak vysoko musí být kosmonaut ,má-li vidět 20% povrchu Země?
5.Urči objem a povrch konvexní čočky,která je průnikem koulí a poloměrech 13cm a 14cm ,jejich středy mají vzdálenost 20cm.
6.Kolik % povrchu ted leží v oblasti pásmu tropického,mírného a polárního?(úhly jsou 2327,6633)
0x
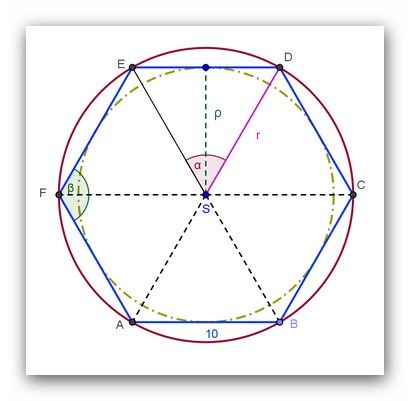
Ad 1.: Poloměr základny je r, průměr je d = 2r, výška válce je rovněž d Úloha je vlastně kvazi stereometrie, stačí vyšetřit poměry v základnovém kruhu, viz přiložený obrázek. Převzal jsem ho odněkud, takže je v něm nakreleno víc, než pořebujeme, ale to nevadí. Jako zkoumanou tětivu můžeme vzít například úsečku ED; má délku r, délky SD a SE jsou rovněž r, takže trojúhelník EDS je rovnostranný trojúhelník s úhly 60°. což je šestina ze 360°. Snadno tedy spočteme délku kratšího z oblouků SD, rovněž obsah výseče dané tím šedesátistupňovým úhlem ESD a když od ní odečteme trojúhelník, máme obsah odpovídající úseče. A jaké je řešení té původní úlohy, to už doufám tazatel zvládne sám.
doplněno 04.12.11 16:27:Pozor, při výpočtu povrchů nezapomenout na obsah toho řezu.
0x
Ad 3. - to snad nemyslíš vážně. Vzorce pro objem válce atd. snad znáš a kdž ne, tak si je najdeš (například aristoteles.cz/...
a dosadíš. Jediné, co by ti mohlo dělat trochu problém, je výška polokoule; tak si řekni, že je to tejí průměr, ne?
doplněno 04.12.11 16:34:Ad 4. Tady zase bydeš potřebovat vzorce pro povrch koule a pro povrch jejího vrchlíku, viz aristoteles.cz/... , a taky poloměr země
(šetři se osle - cojeco.cz/...)
Odsud spočítáš výšku vrchlíku. a k výpočtu výšky pomůže starý dobrý Pythagoras. Je-li na dom ještě něco nejasného (což může být), napiš co a dořešíme.
doplněno 04.12.11 16:54:ad 3 - Překlep, výška polokoule je samozřejmě její poloměr (polokoule je speciální příklad kulové úseče s výškou r).
0x
ad 5. - tady zase použiješ vzorce pro povrch kulového vrchlíku a objem kulové úseče ( sos-souhtyn.cz/...), zde na dva vrchlíky. Jejich výšky jistě spočítat umíte.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.