Nejste přihlášen/a.
Prosím víte někdo jak na tuto úlohu?
Hmotný bod o hmotnosti m=30 kg leží na nakloněné rovině o úhlu ß=45° a je zabržděn. po odbrždění se dá působením své vlastní tíhy do pohybu. Součinitel tření mezi hmotným bodem a nakloněnou rovinou je f. Určete součinitel tření f tak, že po uražení dráhy L=10m dosáhne hmotný bod rychlosti v1=8m/s. Určete velikost zrychlení a, se kterým se hmotný bod pohybuje.
3x
s = ½ at2 = ½ vt vyjádříme t a dosadíme do vztahu pro výpočet zrychlení:
a = v/t = v2/(2s) ; kde s = 10 m dráha, kterou urazil hmotný bod.
Pro sílu platí vztah F = ma; tento vztah dosadíme do té první rovnice:
ma = G sin β – f G cos β
ma = mg sin β – f mg cos β a z této rovnice vyjádřit f snad již potíže činit nebude. Jak je patrné, na hmotnosti nezáleží:
a = g sin β – f g cos β.
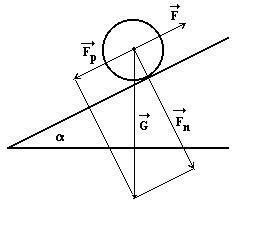
Fp = G sin β. Tato síla je však zmenšena o třecí sílu Ft = f Fn = f G cos β = f mg cos β. Proto síla, která způsobuje zrychlení je F = Fp - Ft = G sin β – f G cos β.
Žádná síla tedy nezmizela, obě jsou zahrnuty v této rovnici: F = G sin β – f G cos β.
A brzdná síla tedy nic neovlivní? Já mám Fn=G*cos ß doplněno ještě o brzdnou sílu F* sin ß ,která působí kolmo na tíhovou sílu
Jaká brzdná síla? Ta ze zadání, o které se praví "a je zabržděn."? Ta po odbrždění zmizí a už nás nezajímá. . Jinak to ale ukazuje na potřebnost na začátku říci, co je co (... kde G je tíhová síla (abych si nemyslel, že jde o tíhové zrychlení), F je..." atd. ) Jinak může vzniknout nedorozumění.
1x
Co potřebujeme vědět? Sílu, působící na těleso ve směru pohybu, tedy ve směru nakloněné roviny.
Jak ji zjistíme? Gravitační sílu rozložíme do směru rovnoběžného s nakloněnou rovinou, a do směru komého. Hledanou sílu zjistíme tak, že od složky do směru pohybu odečteme brzdnou sílu od tření.
Jak zjistíme tuto sílu? Tady zase využijeme tu kolmou složky gravitační síly a součinitel tření.
A co s výsledkem uděláme? Použijeme Newtonovy zákony, respektive pohybovou rovnici. (Trochi si s tím ovšem musíme pohrát.)
dojduk rovnici F=[G*(sinß-f*cosß![]() -m*a]/(cosß*f*sinß
-m*a]/(cosß*f*sinß![]()
ale pak neznám f ani F
doplněno 03.12.11 20:31:místo smajlíka má být konec závorky
Na ty smajlíky jsem zvyklý, to se mi stává taky. Ale k problému: ze začátku neznáte f, to máte nejít, le najít máte i zrychlení a, Sílu F (předúokládám, že máte na mysli tu celkovou sílu znáte v závislosti na f a na a, no a to a zjistíte ze zadaných kinetických údajů, tedu z rovnice pro rovnoměrně zrychlený pohyb: s = ½ at² (začínal jste nulovou rychlostí). No a z Newtonova zákona pak už vpočteme F a z toho f. To by vlastně šlo z té rovnice, kterou jste napsal, problém je v tom, že je špatně (to byste měl poznat už z toho, že nesedí rozměrově, když odhlédnu od toho, že tak nějak vůbec nemá logiku). Jak jste k ní došel?
doplněno 03.12.11 23:04:Koukám, že zatím co jsem to měl rozepsaný a venčil psa a koukal na videostop, petapeta sem napsal podrobné řešení. Ale dva pohledy nikdy nejsou na škodu; jí jsem to tak daleko nedotáhl.
doplněno 04.12.11 13:32:Především se musím omluvit, rozměrově ta rovnice vychází, ta moje poznámka souvisela s tím, že mi nebylo jasné, co je co; G jsem pokládal za gravitační zrchlení, zatím co to měla být přímo gravitační síla, tedy G = m*g, kde m je hmotnost tělesa a g je gravitační zrychlení. To ovšem nemění nic na tom, že ta rovnice je špatně, jen to není tak evidentní. Jak má vpadat, vysvětlil petapeta, takže k tomu se už vracet nemusím. Já jen dodám trochu off ttopic poznámku" ten smajlík na konci vznikne tak, že editor spojí zavírací závorku s nějakým znakem před ní (pomlčka, středník) a čte to dohromady jako smajlík... V našem případě stčedník je součást kodu pro beta (tedy ono je to asi spíš ostré es). Takže chci - li se toho vyvarovat, dělám kolem závorky (jinak nadbytečné) mezery.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.