Ahoj.
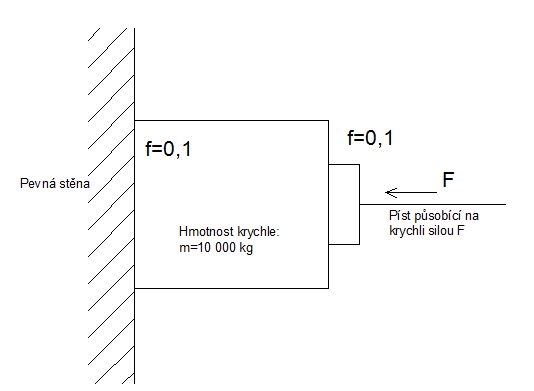
mám tu jeden příklad. Mám krychly o hmotnosti 10 tun, na kterou působí hydraulický píst silou F. Krychle je na druhe straně opřena o pevnou stěnu. Jak velká musí být síla F aby krychle držela mezi pístem a stěnou- aby nespadla (nezklouzla po stěně). Koeficient tření f mezi stěnou a krychlí a mezi krychlí a pístem je f=0,1.
Mě vyšla síla 981 kN. Ale je to asi moc.
1x
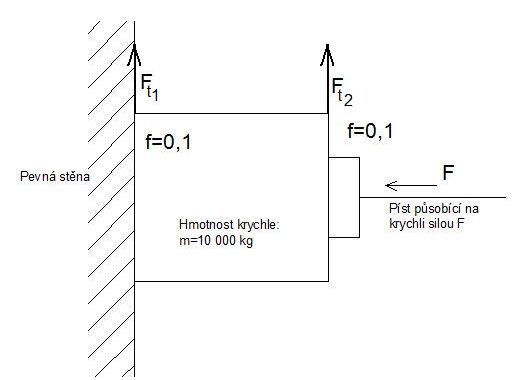
no ale tim padem by byl i tak vysledek stejny. Protoze z rovnice rovnovahy: G=m*g= Ft1+Ft2 =981000 N. Navíc ta stěna nepůsobí na tu krychly žádnou silou.
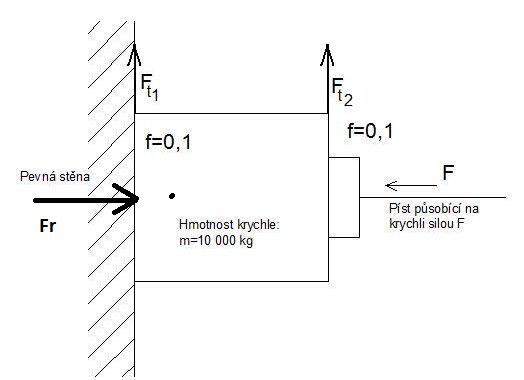
doplněno 24.11.11 14:26:Takze tam ma nejak dodat reakcni sílu od zdi? Fr = F?
Jinak urcite by pak platilo:
Ft1+Ft2=G=m*g=98100N
Podle me kdyz jsou ty koeficienty f stejne tak plati F=Ft * f. Pokud by byl jeden koeficient menší tak by se do toho vzorce dal ten menší.
Uz jsem z toho prikladu zoufalý 
0x
Jde o tzv. smykové tření, viz. google wiki tření. Podle mě:
1/ dolů působí vlastní váha. F1=m*g= 10 000kg * 10= 100kN
2/ kolmá síla je síla válce Fn, F1=f.Fn; tj. Fn=F1/f=100kN/0.1 =1MN
Nevím a nechce se mi hledat, jestli s tím "f" nakládáte správně, možná ano, ale nějak nevidím, že byste uvažovali třecí síly 2: od stěny a od pístu. Je přeci rozdíl, jestli dře (tzn. pomáhá držet) i píst, nebo jen stěna. Nebo ne?
no me to taky vrtá hlavou jestli se tam nepocítá i nejak s třením mezi stěnou a krychlí. Je to celkem stupidní příklad na pohled, ale nejak jsem se nad ním sekl
zákon akce a reakce, jelikož jsou oba koefienty stejné, tak by to mělo být správně, stěna působý na krychly reakční silou, kterou vyvolává píst,
a přepočet na normálovou sílu je Fn=Ft / f
vyšlo vám to oboum stejně, jen hm, použil gravitační zrychlení 10m*s^-2, která zapříčínila ten rozdíl 19kN
dle mého názoru je to takto dobře, žádná věda v tom není
doplněno 24.11.11 09:11: oprava: radarbrdy ne hm
0x
OK, opravuji, včerejší výpočet, nedíval jsem se dost dobře na obrázek Pozorný čtenář si jistě všimnul sám, a upozornil na to...
Třecí plochy jsou dvě, takže síla k udržení bude potřeba poloviční. tj. 1MN / 2= 0,5MN. Obdobně pokud by těleso mělo více ploch, síla k udržení by se zmenšovala. Tj. princip např. viz. wiki lamelová spojka
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.