Ahoj mám takový problém s příkladem
x.(3-x) = 3-i
mám tam problém vypočítat nejspíš diskriminant proto mi to nevychází, nebo spíše myslím že diskriminant mám dobře ale nějak pak nevím jestli mám diskriminant vypočítaný správně, jak s tím teda dál ![]() Děkuji za pomoc
Děkuji za pomoc
0x
x1= 1 _ i
x2= 2 + i
0x
x1= (3+1+2i)/2 = 2 + i
x2= (3 -1 -2i)/2 = 1 - i
Dobře ale jak dostanu ten cos a sin, když udělám -3/5 tak to nevyjde tak abych ten cos mohla najít.
0x
cos α = -3/5 → α = 126,8698976° a dosadíme do vztahu pro výpočet druhé odmocniny:
wolframalpha.com/...
wolframalpha.com/...
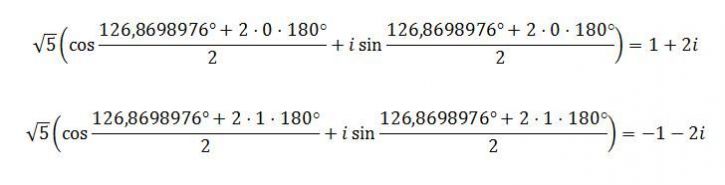
No dobře ale teď mi řekni jak bys z téhle rovnice dostal výsledek bez kalkulačky nebo s normální kalkulou?
A jak určujete hodnoty goniometrických funkcí? Dříve se hledaly v matematicko-fyzikálních tabulkách, dnes hledat v tabulkách umí málokdo.
Většinou nám to právě vychází hezky, takže to počítáme přes cos= a/ absolutní hodnota sin=b/absolutní hodnota to nám vyjde nějak pěkně a pak to můžeme dát do obloukové míry a v pohodě to roznásobit ale tenhle zmetek prostě něvychází ![]()
Úhly nejsou jenom 30°,45°,60°,90°,180°... To při výpočtech nemáte úhly, kdy hledáte hodnoty v tabulkách nebo použijete kalkulačku? On tenhle příklad vychází pěkně, jen ten úhel není celé číslo.
0x
A nešlo by:
odm(D) bude kompl. číslo, takže nějaké A+iB, a tedy D=(A+iB)^2
přitom D=-3+i4, takže -3+i4=(A+iB)^2, -3+i4=A^2+2iAB-B^2
a z toho 4=2AB a -3=A^2-B^2
takže A=2/B, za A dosadíme a dostanem -3=4/(B^2)-B^2, vynásobíme obě strany B^2 a bude
-3B^2=4-B^4, takže B^4-3B^2-4=0 a to vyřešíme jako kvadratickou rovnici (dáme C=B^2 a tedy C^2-3C-4=0)
C vyjde +4 a -1; tu -1 zahodíme, protože nejde reálně odmocnit, C přece =B^2 a B je jen reálné
tak a máme B= +2 a -2 a ze vztahu nahoře 2=AB tedy dostáváme dvě dvojice:
B=2, A=1 a B=-2, A=-1, tedy 2 komplexní čísla 1+i2 a -1-i2 a to jsou ty odmocniny D
No a jsme tam, kde byl(a) petapeta v 1. příspěvku. Že máme dva D (kladný a záporný) nevadí, protože se stejně bere +D i -D, takže nic navíc nemáme.
No, asi to není matematicky nejčistší, měli bychom také ověřit podmínku B=0 (postup platí jen pro B<>0, protože jsme použili A=2/B), jsou tam občas "selské" úvahy (zahodíme -1, protože se nehodí pro reálné odmocnění, na kterém to celé stojí) a tak, ale dá se bez komplexní kalkulačky.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.