Zdravím všechny,
potřebovala bych trochu poradit s tímto příkladem, nehnu s ním. Nebojte, nechci ho vypočítat, není to do testu. Potřebuji jen navést. ![]() Díky moc všem.
Díky moc všem.
2x
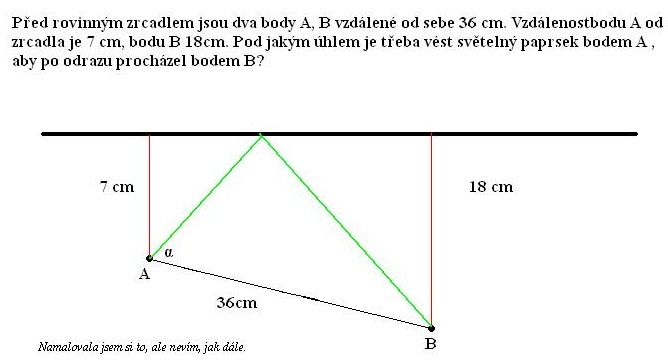
Spočítal bych kolmou vzdálenost těch dvou bodů, 36^2-11^2 = nějakých 34 ^2. Ty dva trojúhelníky v zadání mají stejný úhel (dopadu/odrazu) a druhý mají pravý, tedy jsou podobné, můžu napsat poměr odpovídajících stran, třeba 7/x = 18/(34.3-x), kde x je od pA k bodu dopadu paprsku, vyjde to 9.6. Nakonec ten úhel, tg^-1 (9.6/7) = asi 53.9° (ke kolmici dopadu, ne k zrcadlu).
1x
Já jsem teda na tyhle úlohy nikdy nebyla, ale zkusím to! Třeba aspoň ispiruju!
Já bych si udělala rovnoběžku s tím zrcadlem, která prochází A. Tím vznikne trojúhelník, pravoúhlý, u kterého znám dvě strany a mohu dopočítat třetí. Tím využiju všechny údaje a žádný nebude zbytečně zadaný. :D Ale nevím, k čemu by to bylo.
Když pak tím bodem na zrcadle vedu kolmici k té dopočtené straně, vznikne mi obdélník, složený ze dvou trojúhleníků. Přepona těch trojúhleníků pak bude zároveň úhlopříčkou toho obdélníka. A pro úhlopříčky ve čtverci a obdélníků mají úhel jasně daný. Otázkou je, jestli jsem si to nakreslila dobře a nevyšlo mi to takhle jen náhodou, protože ten náčrtek beztak zkresluje! :D :D
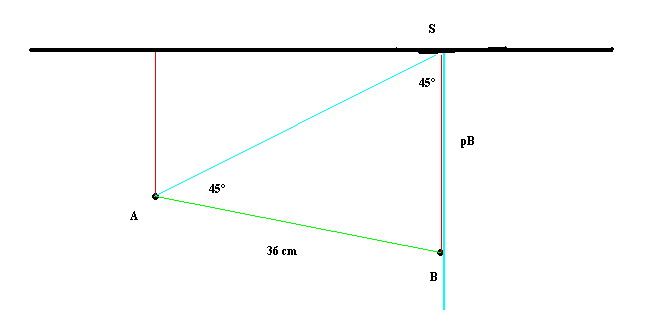
Myslím, že takhle je to dobrý začátek, tedy pokud tomu dobře rozumím. Já bych nejprve doplil označení, abchom se mhli domluvit bes nedorozumění: patu kolmice, spuštěné na zrcadlo z bodu A, bych označil třeba pA, z bodu B ... pB, a průsečík té rovnoběžky se zrcadlem, vedené bodem A, s přímkou B pB treba B1. No a pro úplnost označím bod dopadu na zrcadlo třeba S.
Takže rozumím-kli dobře, chceš (a můžeš) spočítat stranu AB1 trojúhelníka A A1 b. což je zároveň vzdálenost bodů pA, pB neboli vzdálenost obou těch kolmic k zrcadlu.
To je potřebná informace, ale dál už bych se s tím nepáral. Úhel dopadu je roven úhlu dopadu, takže povedu-li body A a S přímku, ta protne tu druhou kolmici, totiž přímku spojující body B a pB, v bodě B¯ , který je zrcadlovým obrazem bodu D. Tobě je to tím již jasné, doufám, že i anzionce.
Jinak možná že i tvůj další postup je správně, já už to nekontroloval, abych nemusel přemýšlet, jaký obdélník a dva trojúhelníky přesně máš na msli.
Tak jedině takhle, jestli je to špatně, tak jsem to bohužel nepochopila. Byl by dobrý náčrtek, protože v těch já jsem dřevo.
doplněno 01.11.11 06:51:Zde:
Zřejmě špatně vysvětluji. Ten první obrázek byllepší, já ho jen doplním a pošlu. (Po snídani.)
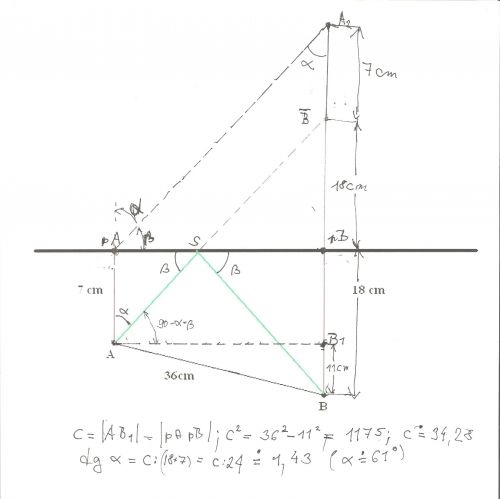
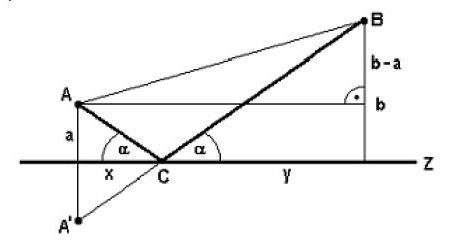
doplněno 01.11.11 10:37:Tak přikládám ten obrázek. Měl by vysvětlovat, co jsem psal já a graficky doplňovat rady Tlapky a Dzordze. Ještě jsem tam doplnil rovnoběžku AA1 s paprskem AS; není to nutné, ale přijde mi to s její pomocí nejjednodušší.
Ještě připomínám, že ß (míním beta, ne ostré s) je úhel dopadu a zároveň, dle zákonů optiky, úhel odrazu.
doplněno 01.11.11 10:39:Pardon, já tu rovnoběžku označil AA2
1x
doplněno 01.11.11 11:29: Než jsem namaloval obrázek, již příklad doplnil Kartaginec. Dopustil se malinké chyby při sčítání 18+7 = 25 a ne 24, proto mu úhel vyšel trochu jinak. Dále podle zadání se měl zřejmě vypočítat úhel PAB, tak to alespoň z obrázku chápu já.
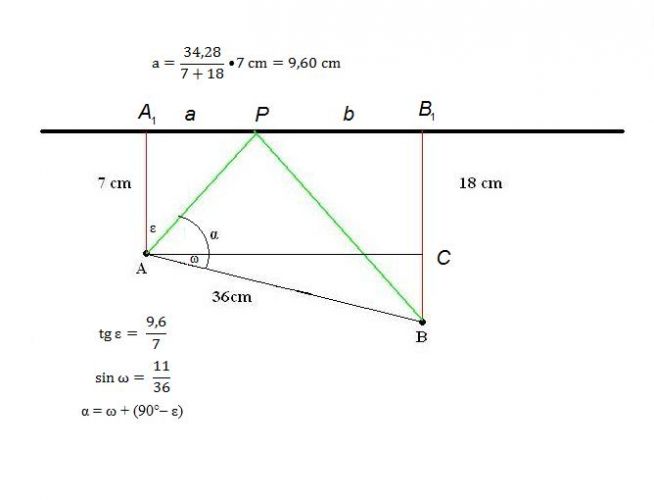
Tak tak, ale vede mne to k otázce, co myslí zadavatel tím úhlem alfa. Podle jeho obrázku to vypadá tak, jak to chápe petapeta, ze slovního zadání to tak jasné není, takže jsem počítal jiný. Ale to je detail, který lze snadno pravit. Jinak s tím sčítáním je to samozřejmě pravda a moc e stydím.
doplněno 01.11.11 11:43:pravit =opravit , moc e = moc se
A to jsem to po sobě četl.
Ono to tam napsané není, takže bez upřesnění bych nepočítal jiný úhel než tenhle
doplněno 01.11.11 12:02:obrázek ..
Před rovinným zrcadlem jsou dva body A, B vzdálené od sebe 36 cm. Vzdálenost bodu A od zrcadla je 7 cm, bodu B 18 cm. Pod jakým úhlem je třeba vést světelný paprsek (jde o úhel mezi rovinou zrcadla a paprskem) bodem A, aby po odrazu procházel bodem B?
Výsledek: 36,1°
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.