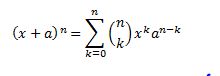Náhodná proměnná

Od: bagryvsb* 30.10.11 16:32

zdravím,

mám tu jeden příkladek. Prosím naléhavě o pomoc. moc

7 odpovědí na otázku

Řazeno dle hodnocení

petapeta*

30.10.11 23:03

Binomické rozdělení lze aproximovat Poissonovým a to v případě, že p < 0,3 nebo p > 0,7:
Bi (n, p) → Po (λ), kde λ = n.p
doplněno 30.10.11 23:09: V Excelu bychom výše uvedenou pravděpodobnost vypočetli pomocí funkce POISSON:
= POISSON(42;40;1) - POISSON(34;40;1) = 0,4679

bagryvsb*

31.10.11 21:20

diky za snahu, ale ja to potrebuji spocitat pocetne a ne v Excelu

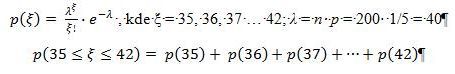
petapeta*

31.10.11 21:41

A co Vám brání, abyste dosadil do vzorce, který jsem uvedl, a vypočítal to.

doplněno 31.10.11 22:03: Nyní si čtu opět zadání a vidím, že máte binomické rozdělení aproximovat normálním rozdělením:
Bi(n, p) → N(μ, σ²), kde μ = n.p, σ²= n.p(1 - p)

Pravděpodobnost pak vypočtete integrováním hustoty pravděpodobnosti v určených mezích (35;42)

bagryvsb*

31.10.11 21:51

a na p < 0,3 nebo p > 0,7 jste prisel kde? Diky za pomoc.

petapeta*

31.10.11 22:38

Ve skriptech
VYSOKÁ ŠKOLA BÁŇSKÁ _ TECHNICKÁ UNIVERZITA OSTRAVA
Pravděpodobnost s statistika; Petr Otipka, Vladislav Šmajstrla

petapeta*

31.10.11 22:43

Tady jsem se pokusil to aproximovat pomocí normálního rozdělení. Pokuste se to zkontrolovat, zdali jsem se při zadávání nespletl.

wolframalpha.com/...

doplněno 31.10.11 23:58:

V excelu mi to vychází stejně:

=NORMDIST(42;40;ODMOCNINA(32);1)-NORMDIST(35;40;ODMOCNINA(32);1)=0,449783636178327

Skočit na otázku
Vložit novou otázku

bagryvsb*

31.10.11 21:56

ja jsem prave myslel ze se to nejak pocita pres Binomickou vetu.

[přidat komentář]

Přidat svou odpověď

Přihlásit se k odběru odpovědí z této otázky:

Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.

Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.