Nejste přihlášen/a.
Mám tento příklad :uhlopříčky kosočtverce jsou dlouhé 24cm a 16cm ,obvod tohoto kosočtverce je 60cm ,ale nevím postup díky za rady.
No ano díky ještě bych potřeboval vědět jaký vzorec použiji (path.větou) dosadit ,abych to viděl díky
takzeale a (na druhou)=u1 (pul na druhou ne) u2(pul na druhou ne?) Jinak uz vim vcem byl problém já debil to nedal na druhou:D
Hele jeste ktomu prvnimu prikladu A(nadruhou)=u1(půl na druhou) +u2(pul na druhou) my vyslo a(na druhou)=288+162=450a to když odmocním a vynásobím 4 není 60![]()
4*√(12^2 + 8^2) = 4*√208 = 57.7 a to opravdu není 60 ![]() Jestli ony ty úhlopříčky náhodou nejsou 24 a 18?
Jestli ony ty úhlopříčky náhodou nejsou 24 a 18?
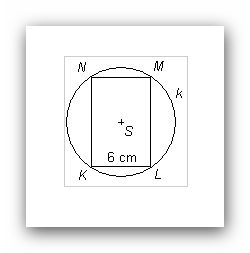
jeste tu mam asi 3 priklady ![]() kružnice k opsaná obdelníku klmn na obrázku má střed v bodě S a poloměr 5cm .obsah obdelníku klmn je 48cm ,ale dolní a horní strana obdelníku má 6cm a boční strany nevím nevíte postup?díky
kružnice k opsaná obdelníku klmn na obrázku má střed v bodě S a poloměr 5cm .obsah obdelníku klmn je 48cm ,ale dolní a horní strana obdelníku má 6cm a boční strany nevím nevíte postup?díky
Podíval jste se na obrázek? Kde nejlépe vidíte poloměr té kružnice?
Jak zní vůbec otázka? Ten obsah obdélníku se mi opět zdá být nadbytečnou informací.
ano díky,ale potřebuju to vysvětlit ,jakým způsobem to mám vypočítat ty dvě strany které neznám díky
No dzordz uvedl hned dvě možnosti: jednak tu, že obsah je součin sran, takže jedna strana je obsah dělený tou druhou, a dvak, že úhllopžíčka obdélmíka je přeponou pravoúhlého troúhelníka se stranami rovnými stranám obdélníka. On to nenapsal takhle naplno, v domění že by vám to mělo stačit, ale asi ne, tak takhle je to trochu úplnější. To už jistě stačí, ne? Jen ještě ono je to zkutečně přeurčené, buď obsah, nebo poloměr jsou tam navíc. Nebo je navíc ta délka jedné strany, čemuž by nasvědčovala věta ,jakým způsobem to mám vypočítat ty dvě strany které neznám díky. To by bylo trochu (ale ne zas moc) složitější, nicméně jaké je tedy přesné zadání, co je známo?
Kružnice k opsaná obdélníku KLMN na obrázku má střed v bodě S a poloměr 5 cm. Obsah obdélníka KLMN je
Jinak můžete mi blíže vysvětlit jak vypočítám strany ,když použiji způsob s trojuhelníkem?díky
Takže strany neznám, označme je a, b. Obsah V = 48 cm² je tedy zadán, ale strany a, b nikoli, je to tak? A odkud tedy víte, že jedna strana je 6 cm? No nic, vycházím z toho, že předem známa neí, takžr počítám V = ab, d² = a² + b², kde d je průměr, teda 10 cm, a zároveň odvěsna rojúhelníka KLM, takže mám dvě rovnice pro dvě neznámé. Tu umíte? Jsou jvadratické, ale zase tak těžké by to bát nemělo.
A teď restaruju comp.
Tak znovu: jak zní zadání?
Jinak v tom, co jsem psal před chvílí, naleznete odpověď v každém případě, jen si musíte vyjasnit, co znáte.
Tak tomu zase nerozumím. Proč chceš počítat obsah, když ho znáš? A pokud chceš počítat strany, to jsem sice popsal, ale jak to udělat bez rovnic o dvou neznámých, moc neví. No nic, něco napíšu, ale po restartu .
doplněno 28.10.11 21:12:Takže takhle: předvedu to abstraktně a na tom prvním případu. Pro změnu ale místo a, b označím strany obdélníka x, y: |KL| = x, |LM| = y; dále znám |KM | = d = 10 (podrobně viz dzordz níže). Dále vím, že obsah V je roven součinu stran : V =, a Pythagorova věta říká, že
x² +y² = d² = 100. Jde tedy o dvě rovnice:
x*y = V
x² +y² =100
A teď je otázka, co s nimi? Sice jste se rovnice o dvou neznámých neučili, ale lze to vymyslet: z první rovnice vidím, že y =V/x, dosadím do druhé a mám x² + V²/x² = 100, čili x^4 - 100x² + V² = 0. Tady je ale háček v tom, že je to rovnice čtvrtého stupně, tak to chce trochy přemýšlet. Zavedu si pomocnou proměnnou ("substituci") z = x² , takže x na čtvrtou je rovno z² a dostanete pro z kvadratickou rovnici, která seřeší podle vzorce. Ten buď znáš a tak netřeba, abych ho uváděl, prostě do něj dosadíte. Nebo jste se ho ještě neučili a pak zase nemá moc cenu ho sem psát; prostě existuje.
Existuje ale i jiný postup. Ten používá chytrý trik, na který bys bez zkušeností asi nepřišel, ale když ho sem napíšu, bude snad pochoitelný.
První rovnici vynásobím dvěma a jednou ji k té druhé přičtu, ednou odečtu. Tahže dostanu zase dvě rovnice:
x² + 2xy +y² =100 + 2V (v příkladě A ze zadání x² + 2xy +y² = 220 , v případě B x² + 2xy +y² =196 = 13²)
x² - 2xy +y² = 100 -2V (v případě A x²- 2xy +y² = - 20, v případě B x² - 2xy +y² = 4= 2² ).
A už to začíná být moc dlouhé, odešlu to a zbytek napíšu, až vyvenčím psa, zatím o tom můžete přemýšlet.
doplněno 28.10.11 22:04:Pardo, překlep, x² + 2xy +y² =196 = 14² . Ten smajlík se tam sice dostal omylem, ale měl pravdu.
OHele takhle narovinu to jsou zkušební testy tak jsem si řekl procvičím jsi to ,odpovědi byli na konci stránky,ale k čemu mi je odpověd ,když neznám postup že?jinak můžete mi napsat výpočty té rovnice nebo něco jak bvych to mohl pochopit?díky
Tak máte tam ten obdélník, který má vyznačeno 6cm na kratší straně. Pak je tam ta opsaná kružnice, která má poloměr 5cm. Ten budete nutně potřebovat, jen v tom obrázku není tak úplně "vidět" a vy ho tam zřejmě také stále nevidíte. Spojíte tedy střed S s jedním z vrcholů, třeba K. K leží na kružnici, jeho vzdálenost od S je tedy také 5cm. S můžete spojit i s M, tam bude vzdálenost taky taková.
Teď už tam máte trojúhelník KLM, znáte stranu KL (je tam napsaná), znáte stranu KM (z výše uvedeného to je 5+5cm), úhel u vrcholu L je pravý (z toho obdélníku). Takže spočítat délku LM už nebude problém. No a nakonec vynásobíte |KL|*|LM|, tedy obsah bude 6*8.
Asi hodně blbá otázka ,ale jak vypočítám teda tu stranu LM ,když je ten úhel pravoúhlý?díky
Tak to zkusím dopsat. Zatím jsme se dostali k tomu, že máme dvě rovnice, x² + 2xy +y² = M. x² - 2xy +y² = N (M,N jsem napsal jako zkratku za ty pravé pravé strany) Pokud jsi o tom přemýšlel, moýná ti levé strany připomněly binomickou poučku. Měli jste ji? Když ne, nevadí, napíšu ji sem. Skutečně,
x² + 2xy +y² = (x+y)²
x² - 2xy +y² = (x-y)²
(to je právě ta binomická poučka)
No a když ty rovnice teď odmocníš, dostaneš (x+y) = O, (x-y) = P. kde O je odmocnina zM, P je odmocnina z N. Dál to ukážu na těch konkrétních případech.
Zadání A: zde bude N = -20 a záporná čísla nelze odmocňovat, zadání nemá řečení.
Zadání B: tady nám vyjde x+y = 14 (nebo taky -14, ale protože x,y jsou délky stran, tato možnost nepřichází v úvahu), x-y = 2 (nebo taky -2, ale tenhle případ nechám na tobě). Když obě rovnice sečteme, dostaneme 2x = 16, x = 8; a když je odečteme, dostaneme 2y = 12, y = 6.
BTW ohodnotil bych ještě i ty poslední dzordzovy odpovědim, ale už nemám volné body.)
- Popis konstrukce kružnice opsané a vepsané
- Těžký přiklad
- Kružnice vepsaná
- Thaletova kružnice?
- Rovnoramenný lichoběžník+kružnice opsaná
- Zajímavé úlohy
- Kružnice opsaná poloměr
- Opsaná kružnice u trojúh. nelze narýsovat?
- Konstrukční úloha
- Úkol do matematiky - 5-ti cípa hvězda
- Plášt rotačního válce
- Délka strany čtverce
- Kružnice vepsaná, opsaná osmiúhelníku
- Logaritmus definiční obor
- Příklady - vektory
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.