Zdravím,
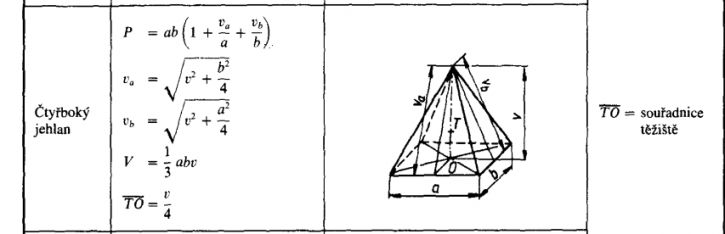
chtěl bych Vás poprosit jestli neznáte vzorec pro povrch pravidelného čtyřbokého jehlanu. Na internetu je pouze ten základní a já bych potřeboval už ten upravený. Předem děkuji 
Na konci minulého školního roku jsme začali dělat stereometrii a hned nás upozorňovali, že tento vzorec používat nemáme a psal nám nějaký dlouhý a celý rozložený... Jenže teď máme jiného učitele a ten mi vzal sešit, aby se koukl, jak jsme na tom. A ejhle, naložil nám plno úkolů a já nemám do čeho nahlédnout a na internetu jsem žádný takový jaký nám pan učitel psal není k nalezení, takže jsem zvolil tento způsob, jestli ho někdo z Vás nezná
0x
Ono je to těžké, poradit vzorec jen na základě toho, že má být jiný, než nějaký, který taky neznáme. Ten vzorec, který uvádí pawlik, je samozřemě dobře, ale je pro obecnější jehlan než pravidelný, záhladna je sice obdélníková, ale ne nutně čtvercová. Takže to může být ono, ale taky nemusí, pokud to má být vysloveně pro pravidelný čtyřboký jehlan. Jinak samozřejmě záleží na tom, z jakých údajů vycházíme. (Múžeme znát stranu(strany) základny a k tomu tělesovou výšku, nebo stranovou výšku, nebo boční hranu, nebo i něco jiného, a podle toho se budou vzorečky lišit, a tak podobně. Pro začátek by možná pomohlo, kdybys napsal, co myslíš pod "základním" vzorcem.
Zakladni vzorec je IMHO ten nejvice obecny, ktery plati pro vsechny zadane pripady. Tim ale nemyslim, ze bych sem napsal, ze P=suma integralu jednitlivych stran . Mimochoem pocitat povrch jehlanu z toho, ze znam jednu ze sten a jeji uhel odklonu muze byt pekny opruz. To snad na strednii neberou.
Nojo, i tak se na to lze dívat; jen které jsou ty zadané případy. Vlastně každý vzorec platí pro všechny zadané případy, nebo je špatně. S tím integrálem to ovšem není zase takšpatný nápad; vlastně to je to, co uvádí třeba i Wikipedie:
Povrch jehlanu se vypočítává jako součet obsahu základny a obsahu jednotlivých trojúhelníkových stěn - jejich počet je dán počtem stran základny:S = P+Q, kde P je obsah podstavy a Q je obsah pláště.
To je dost obecné a v této syrové podobě málo použitelné. Mne by hlavně zajímalo, co tím "základním vzorcem" myslí sám tazatel. Taky bych pak lépe pochopil, proč ho nemají používat; takhle neurčitému zadání moc nerozumím.
Jinak to, pocitat povrch jehlanu z toho, ze znam jednu ze sten a jeji uhel odklonu, mne zaujalo jako výzva, pro mne, ne pro tazatele, s tím, že něco takového nejspíš asi nebrali, docela souhlasím. Zatím jsem ale zůstal viset na tom, co znamená, znátm jednu ze stěn.
No to je fakt, ze na wiki je to taky obecne.
K vasemu dotazu; Znam jednu ze sten - znam treba jeji povrch a vysku, nebo povrch a uhel v jednom vrcholu nebo jinou kombinaci, ktera mi dokaze zadefinovat povrch trojuhelnika. Kdyz nad tim tak dumam, tak je to vsechno resitelne vzorcem na obsah trojuhelnika + sinova nebo kosinova veta.. No a phytagoras samozrejme,
To máte zadáno nějak málo. I když budete o trojúhelníku vědět vše, pořád ještě nevíte, jaký je jehlan. Potřebujete jeden úhel nebo jednu délku navíc.
No jo, na tom něco je. Zřejmě mluvíme o pravidelném čtyřbokém jehlanu, aby stačila jedna ze sěn. Pak ovšem dva údaje o té stěně asi budou stačit a ten sklon už bude nadbytečný; třeba v tom prvním případě ze stěnové výšky a obsahu spočtu základnu trojúhelníka, čili stranu základny jehlanu (základnovou hranu) a vím vše. Složitější by bylo, znát třeba výšku sěny a sklon, ale zase ne tak moc, v podstatě dvě protilehlé výšky tvoří rovnoramenný trojúhelník se známou stranou a úhlem při základně (a tedy znám všechny úhly) a jeho základna bude tvořit střední příčku čtvercové základny jehlanu, která je stejné délku jako strana této základny.
Co mi zatím není úplně jasné, je, jak by se to řešilo kdybych znal jen úhel náklonu a obsah toho trojúhelníka. Stačit by to mělo, ale jak, to sice trochu tuším, ale musel bych si to napsat a rozhodně by to bylo komplikovanější než ty dosavadní případy.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.