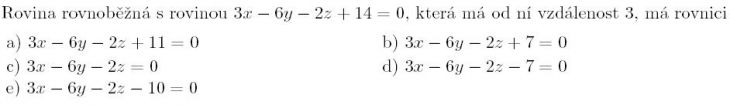Nejste přihlášen/a.
3x
Vzdálenost bodu od roviny je
s = | ap1 + bp2 + cp3 + d | / sqrt(a² + b² + c² )
koeficienty p1 p2 p3 jsou souřadnice bodu
koeficienty a b c d jsou koeficienty obecné rovnice roviny.
Potom bych na zadané rovině určil libovolný bod a zkusil vypočíst vzdálenost tohoto bodu k uvedeným rovinám a jistě se dopátráme která rovina je vzdálená od tohoto bodu právě 3.
doplněno 06.06.11 15:12:Kolega přede mnou pěkně tlápnul vedle. Podle něho by měla vyhovavat ta první rovnice, ale není tomu tak.
doplněno 06.06.11 15:15:Bez nějakého "zkoušení" mohu hned za "s" dosadit číslo 3 a koeficient "d" bude neznámá "x" a lehce vypočteme která rovnice zadání odpovídá.
Odpovídal by i koeficient d=35 ovšem taková rovnice s uvedeným koeficientem v zadání není.
Idea je správná až geniální, postup více méně taky, a skutečně rovina s d = 35 je vzdálená 3, na jednu stranu. Ale při odstraňování abs. hodnoty máme dvě možnosti, ponechat vnitřek tak, jak je (to vyjde těch d = 35) nebo změnit znaménko, čímž najdeme rovinu vzdálenou o 3 na druhou stranu, a tam vyjde d = -7. (Mimochodem stojí za výslovné upozornění, že nemusíme nutně určovat konkrétní bod dané roviny, protože 3x -6y - 2z = -14 pro každý takový bod; tak asi Jirbar postupoval, jen to neřekl nahlas.)
Jistě. Stačí si vymyslet souřadnice X=1 Y=1 pak již vyjde Z=5,5. No a řešení že d = -7 mi pochopitelně vyšlo, jen jsem to nechtěl tazateli zjednodušovat.
doplněno 06.06.11 18:47:A jen tak mimochodem, psal jsem o libovolném bodu.
No tak to se omlouvám. Ale ono to bylo trochu matoucí, skoro by pak bylo jednodušší ten výsledek nenapsat vůbec, ale takhle to bylo záludnější a na tu záludnost jsem skočil sám.
doplněno 06.06.11 18:50:Nevšiml jsem si totiž v extu: tomu by odpovídal výsledek i 35
Vždyť se nic neděje. Totiž někdy to je slovíčkaření a fakt je, že by se mělo jít až do programátorské logiky. Taky bych neměl psát "Libovolný bod" ale mělo by to být "Libovolný bod ležící v zadané rovině". Jenže logika předpokladu by snad mohla taky stačit.
doplněno 06.06.11 19:08:Ovšem na pováženou je, že se diskuze nezúčastňuje především autor dotazu.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.