Zdravim,
zítra jdu na test z analytické geometrie - kružnice.
Sepsala jsem pár nejasností -
Obecny tvar rovnice: x^2 + y^2 + 8x - 10y - 75 - 0
Ma se to prevest na stredovy tvar.
Reseni je x^2+8x+16-16+y^2-10y+25-25-75=0 atd...
Není mi jasné, jak tam přišli na těch +16-16 a +25-25. Kde se to tam vzalo, odkud a jak?
A pak by mě zajímalo, proč rovnice (x-1)^2 + (y+2)^2 = -2 není středovým tvarem rovnice kružnice?
A prosim po lopatě, jako blbci, protože na to koukam jak tele na nový vrata a vůbec nepobírám, takže každá rada dobrá
.
Díky,
Vlk.
3x
K druhé otýzce: Víte, co podle definice znamená to číslo na pravé straně rovnice? To je poloměr té kružnice na druhou. A poloměr, kór na druhou, přece nemůže být záporné číslo. To je všechno. 
A k první otázce: tam si nejsem jistá, já tyto úlohy řeším trošku jinak, asi přeskakuju ten krok, který máte vy zapsán. Převádění z obecné rovnice na středovou se provádí doplňováním na čtverec, tzn. podle vzorce (a+b)^2 nebo (a-b)^2.
Takže to x^2 + 8x si zřejmě zapisujete jako x^2+8x+16 -16 (protože za doplněním na čtverec vždy odečteme b^2). Ve druhém kroku by pak výpočet měl vypadat (x+4)^2 -16... podobně tak situace u y.
A proč zrovna 16? Protože ten vzorec (a+b)^2 se rozepisuje jako a^2+ 2ab+ b^2. Pokud 2ab=8x a a=1x, tak b bude rovno čtyřem.
Snad jsem to vysvětlila dobře...
potěšení na mé straně 
Zítra z toho píšu čtvrteletku, tak otestování znalostí z jiného soudku než knihy se hodí... :D 
0x
když je x^2 a 8x pak vlastně doplněním na vzorec A^2 + 2AB + B^2 = (A+B)^2 musíte přičíst těch 2x8=16 ale zárověň je odečíst aby se strany rovnice rovnaly, nebyly změněny příkladem X^2 + 4X = 0 převedu na tvar X^2 + 4X + 4 = 4 kde k oběma stranám rovnice jsem přičetl 4 a dále se do dá přepsat na (X+2)^2 = 4. středový tvar kružnice si najděte v učebnici ... odpověď 2 je že -2 nemůže být poloměr na druhou protože poloměr na druhou není nikdy záporné číslo.
0x
Ještě pro úplnost doplním, že levá strana ve středovém tvaru kružnice představuje podle Pythagorovy věty vzdálenost obecného bodu [x,y] od středu . Obecně
(x-m)2 + (y-n)2 = r2
je středový tvar kružnice s poloměrem r a středem o souřadnicích [m,n]. Srovnej vložený obrázek, na kterém trojúhelník SMX je pravoúhlý, délka strany SM je x-m, délka strany XM je y-n a |XS| = r, takže ta rovnice kružnice je skutečně Pythagorova věta. Ono je to tu obsaženo na pozadí příspěvků, všichni to vědí, ale explicitně to nezaznělo.
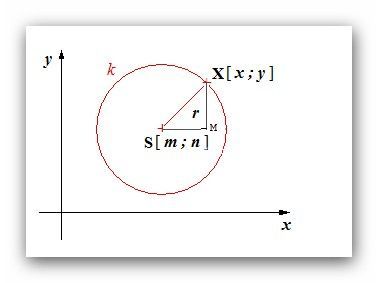
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.