Nejste přihlášen/a.
Dobrý den,
neumím vyřešit níže uvedené ulohy, a tak se obracím na Vás. Nevím, jak to tu funguje, ale pořeboval by jsem vysvětlit (nejsem žádný matikář, tak prosím co nejvíc tzv. po lopatě, děkuji za pochopení) postup výpočtu. Znám výsledky úloh, ale nedokážu se dobrat k výsledku. Dofám, že mi s tím někdo pomůžu, byl bych velice moc vděčný! ![]()
PS: Mohl bych poprosit, jestli by třeba nemohl také někdo udělat náčrtky např. těch krychlí, koulí atd. Stačí jen načrtnout, vyfotit a poslat na email ( j3n4@seznam.cz) Moc by mi to pomohlo s úkolem. Předem děkuji za ochotu.
1. Ruční porcovač zmrzliny zformuje 5 cl mraženého krému do polokoule. Jak velký je průměr této polokoule? [58 mm]2. Čtverec se stranou délky 6 cm se otáčí kolem úhlopříčky. Jaký je objem vzniklého rotačního tělesa? [36pí √2 cm3]
3. Je dána krychle ABCDEFGH. Odchylka přímek EG a BG je? [60 stupňů]
4. Součet obsahů obou podstav válce o výšce 7 cm je roven obsahu jeho pláště. Jak velký je objem tohoto válce? [343pí cm3]
5. Je dána krychle ABCDEFGH s hranou délky 1 dm. Vzdálenost bodu od přímky AC je? [jedna poloviny √6 dm]
6. Nádoba, která má tvar pláště rotačního kuželu a je zaplněna vodou do jedné poloviny své výšky. Poměr objemu vody a objemu nádoby je? [1 : 8]
7. V krychli ABCDEFGH je bod K středem hrany AB a bod L středem hrany FG. Pro odchylku alfa a přímek KL a FG platí?
[tg alfa = √5]
8. Zvětší-li se poloměr koule o 50 %, o kolik % se zvětší její povrch o? [125 %]
9. Středy hran krychle o hraně délky 1 dm tvoří vrcholy čtrnáctistěnu. Objem tohoto čtrnáctistěnu je? [pět šestin dm3]
10. Tři míčky jsou uloženy v plechovce tvaru válce (na sobě), navzájem se dotýkají a dotýkají se i stěn plechovky. Poměr objemu všech tří míčků a objemu plechovky je?[2 : 3]
11. Střecha sportovní haly má tvar poloviny rotační válcové plochy, výška příslušného válce je větší než jeho průměr. Obsah střechy je 433 m2. Jestliže poměr délky a šířky haly je 8 : 3, jsou tyto rozměry přibližně? [27,1 m a 10,2 m]
12. Poloměr koule opsané dané krychli je k-krát větší než poloměr koule této krychli vepsané, kde? [k = √3]
13. Do krychle ABCDEFGH je vepsán čtyřboký jehlan PQRSV tak, že jeho hlavní vrchol V je středem stěny EFGH a vrcholy P, Q, R, S jeho podstavy jsou středy hran AB, BC, CD, DA Poměr objemu jehlanu a objemu krychle je? [1 : 6]
2x
Pro začátek návod na první dva:
1.Tady si myslím, že náčrtek zde netřeba, vem si třeba míč. Nebo se podívej na cs.wikipedia.org/... a na cs.wikipedia.org/... Příklad sám je jednoduchý, Vzorec pro objem koule snad znáš (V = (4/3) * pí r^3, slovy čtyří třeniny pí er na třetí), polokoule je polovic a průměr je dvojnásobek poloměru. Objem znáš _ je 5 cl, to si převeď na milimetry kubické, a pak z uvedeného vzorečku vypočteš poloměr a následně průměr . (Zkus a když to nevyjde, napiš, předveď, opravíme.)
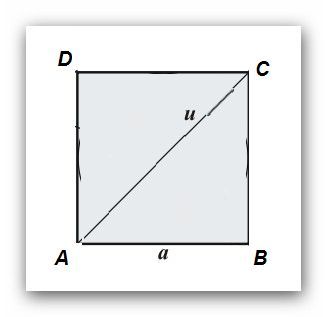
2. Úhlopříčka u = AC čtverce ho dělí na dva trojúhelníky (viz přiložený obrázek), čtverec má dvě k sobě klolmé úhlopříčky, tu druhou v tom obrázku nakreslenou nemáš, Když ho necháš rotovat kolem té nenakreslené úhlopříčky BD , pak trojúhelník ACD vytvoří rotační kužel (viz cs.wikipedia.org/... s výškou rovnou polovině úhlopříčky BD a s pruměrem základny rovným úhlopříčce AC. Ten druhý trojúhelník vytvoří stejný kužel, ale obrácený špičkou na opačnou stranu. Znáš stranu, tak spočítáš úhlopříčku (vzorečky jsou v té Wikipedii) a odsud spočteš objem těch dvou kuželů. na to jsou vzorečky v kle.cz/...
V tom návodu by mělo být vše podstatné, pokud nicméně to potřebuješ ještě více polopatě, napiš, co není jasné, a můžu to rozvést. Ale nejdřív to zkus, abych věděl, co mám doplnit.
5cl = 10 000 cm3 a když to dám do rovnice: 10 000 = 4/3 * 3,14 * r3 (mám tuto rovnice vynásobit 3?, nemůžu se prostě dopočít, kde dělám chybu?)
A úlohy č. 2, tu vůbec nechápu... nevím co vlastně počítám a jaký použít vzorečky (je to vysvětlené dobře, ale já prostě geometrii a nějak si představit něco v tom obrazci za tvar...tohle bohužel nechápu...)
Možná jde o nedorozumění ve značení, stříška znamená mocnění, čili ale to jsem tam psal slovy. Jinak převod: 5 cl je pět setin litru,1 litr je decimetr kubický čili 10^3 [cm^3] , centimetr je deset milimetrů, čili litr je 10^3 *[10^3 mm^3] = 1000000 [mm^3] a centilitr je
10 000 [mm^3] , 5 ml = 50 000 [mm^3]; to je první chyba. Na druhou stranu, ty jsi použil vpravo vzoreček pro obsah celé koule a těch 5 ml je polokoule, takže správná rovnice je
100 000 = 4/3 * 3,14 * r^3
odkud r^3 = (3*100000)/3,14159
z výsledku musíš udělat třetí odmocninu (to je možná(?) druhá chyba) , čímž dostaneš r a dvojnásobek je hledaný průměr. Přepočítával jsem to a to by mělo víceméně (po zaokrouhlení) vyjít.
K dvojce se případně vrátím později, zkusím vymyslet nácornější obrázek.
2x
Ad 4.: Viz cs.wikipedia.org/... Ve vzorečcích pro obsah Q pláště a obsah S celého povrchu je h = 7 známá výška, r zatím neznámý poloměr základny. Ze zadání plyne (při použití označení, které je ve Wikipedii použito úplně nakonec pro rotační válec)
Q = S - Q,
po dosazení tedy
2(pí) r h = 2(pí) r²
rh= r²
a tedy r =?
doplněno 02.04.11 20:16:No a objem dostaneme dosazením r do vzorečku, který tam taky je.
Vyšlo mi r = 7 a objem mi také vyšel, děkuji za tento příklad ![]()
Dále jsem počítal, ale nedopočítal... jediné co mi ai vyšlo je příklad č. 8 : bral jsem to jaksi rozumě, když celek je 100 dílků a r = poloměr a zvětší se o 50% = 25 dílků a těch 100 dílků + 25 dílků je 125 %. Moc to matematické není, ale dává mi to aspoń smysl, je to dobře?
No je to špatně. Právě jsem vysvětlil proč, ale než jsem to stačil odeslat, povedlo se mi to zmazat, znovu to napíšu později.
doplněno 04.04.11 19:58:Tak abych to doplnil: ta úvaha je nějaká scestná. Co bereš za sto dílků? Ten poloměr? Ale potřebuješ vědět, o kolik procent se zvýší povrch, a to jsou zase jiné dílky. A padesát procent ze sta dílkú přece není 25 dílků. Atd.
Postup je takový: povrvh koule o poloměru r je roven 4 pí r^2 (připomínám, že r^2 znamená r na druhou). Odsud vidíš, že když se poloměr zvětší k krát, povrch se zvětší k na druhou krát, z toho je třeba vyjít. My ovšem nemáme zadáno, kolikrát se se zvětší, ale o kolik, tak to převedeme: zvětšení o 50% je zvětšení o polovinu, tedy jeden a půlkrát (k = 2,5)(chceš-li, tedy ze sta dílkú - procent, na stopadesát, vyjde to nastejno. ) Teď, 1,5^2 = 2, 25, čili povrch se zvětší 2,25 krát, čili o 1,25 původního povrchu. Zvětšení povrchu v procentech počítáme ovšem tak, že za sáklad bereme původní povrch o (= 100%), ten se zvětší o 1,25 o, což je těch 125 %.
0x
Ad 3.:
Přímky EG a BG jspou prodloužené strany rovnostranného trojúhelníka EGB (jehož strany jsou stěnové úhlopříčky krychle, viz přiložený obrázek). No a jaké úhly má rovnostranný trojúhelník?
doplněno 02.04.11 19:41:Než se podívám na příklad 5, doplňte prosím: vzdálenost kterého bodu od uvedené přímky máme určovat?
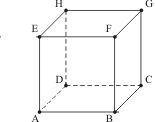
Ten 5. př. zní určitě takto: Je dána krychle ABCDEFGH s hranou délky 1 dm. Vzdálenost bodu F od přímky AC je?
nebo:Je dána krychle ABCDEFGH s hranou délky 1 dm. Vzdálenost bodu H od přímky AC je?
0x
Ad 6: To je v principu podobné jako ta osmička. Základní mmyšlenka je ta, že když máš dvě podobná tělesa (podobná ve smyslu geometrické podobnosti), takže jedno má všechny odpovídající rozměry rovné k-násobku druhého, tak plošné veličiny (obsah povrchu, u kužele třeba obsah základny atd) se zvětšují k^2 krát a objemy se násobí třetí mocninou toho k, podobně jako jsme to dělali u koule.
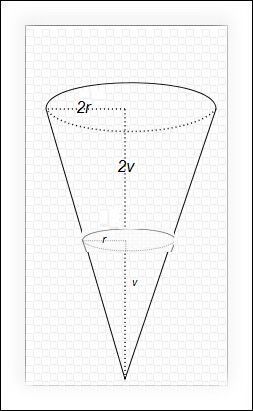
V uvažovaném příkladu konkrétně (viz přiložený obrázek):
část kužele, naplněná vodou, je podobná celé nádobě. Výška toho naplněného kužele budiž v, pak výška celého kužele bude 2v. Podobně poloměry kruhové základny budou r a 2r. A abych nemusel pořád vypisovat pí slovy, použiji pro něj značku ¶, užívanou pro odstavec: ¶ = 3,141592... (Je to blbé, ale snad si budeme rozumět; je to nejpodobnější, co jsem v editoru našel.) Pak obsah kužele je jedna třetina základna krát výška. U té části naplněné vodou je to
V1 = (1/3)(¶ r² *v) = r² *v *(¶/3)
no a obsah celého kužele je:
V = (2r)² *(2v) *(¶/3) = 8*V1.
Jasné?
jo jasný! To mi vyšlo, takže zatím dobrý, děkuji, až na ten přáklad 2, ten mi pořád nějak nejde vypočítat (tam se musí použit pythagorova věta ne...?
No je potřeba znát délku úhlopříčky. Lze samozřejmě použít hotový vzorec, ale ten se skutečně odvozuje z Pythagorovy věty. Dobře je to vidět na obrázku z mé první odpovědi.Úhlopříčka u čtverce ABCD je odvěsnou pravoúhlého rovnoramenného trojúhelníka ABC, jehož obě odvěsny jsou rovny a.Podle Pythagora tedy platí
u² = a² + a² = 2a²
u = a V¯2
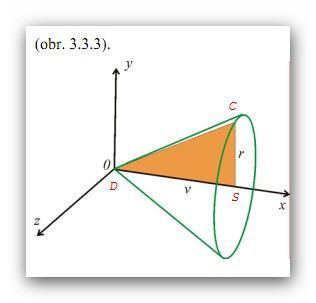
Druhá věc je, jak tuto délku využít, čili základem je představit si, jaké tělěso rotací kolem úhlopříčky vzniká. Možná pomúže k té představě obrázek 3.3.3 na stránce homen.vsb.cz/..., (pokud se mi podařilo sem dát odkaz) ale zdaleka to není přesně ono; upravím ho a znobu napíšu.
Ten odkaz co byl vložen, tak mi nejde, nechce mě to pustit... a k tomu příkladu, když teda u= a√2 , tak to dosadím jen do vzorečku objemu?(V= ¶*r^2*v /3). Výsledek je 36¶ √2 cm3, to jako nebudu dosazovat za to pí, aby mi to takhle vyšlo...
Zde je obrázek, na který @kartaginec odkazuje:
doplněno 08.04.11 14:46:Znakem ¶ rozumí kataginec π (= přibližně 3,14)
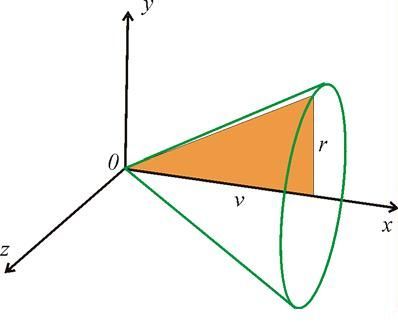
Přesně tak (ostatně jsem tuto úmluvu někde výše avízoval). A je to i ten obrázek, já ho chtěl malinko upravit, aby lépe korespndoval se zadáním. Takže (viz přiložený obrázek):
Vrať se k mému úplně prvnímu obrázku (čtverec ABCD sezakreslenou úhlopříčkou AC) a doplň si do něj ještě úhlopříčku BD a střed (průsečík úhlopříček) S. Představme si, že čtverec rotuje kolem úhlopříčky DB. Pro začátek se soustředíme na "horní polovinu", trojúhelník ACD, (ta druhá polovina bude podobná) a přejděme teď k obázku, vloženému k této odpovědi. V něm je vyznačen barevně vyplněný trojúhelník DSC (druhou část, trojúhelník DSA, si tam snadno domyslíš, zároveň ale vidíš, že se na ni můžeš i vykašlat, protože ho zastoupí ta nakreslená půlka _ když ji otočíš kolem osy x o 180 stupňů, zaujme jeho místo). Ten obrázek sice neodpovídá poměrem stran (je to ostatně obrázek k něčemu jinému), ale jako náčrtek to snad postačí. A vidíme, že velikosti v a r u nás odpovídají polovině úhlopříčky u:
v = r = u/2
No a teď už to musí být jasné: trojúhelník DSC rotací vytvoří kužel, jehož základna je kruh o poloměru r = u/2 a tedy o ploše
S =π (u/2)^2 a o výšce v = u/2, který má objem (1/3) S*v, a stačí dosadit (znak π jsem si tentokrát vypůjčil od petapeta).
Ten druhý, zatím vynechaný trojúhelník ABC vytvoří stejně velký, jen obrácený kužel, takže předchoxí výsledek zdvojnásobíme.
0x
Příklad 9.:
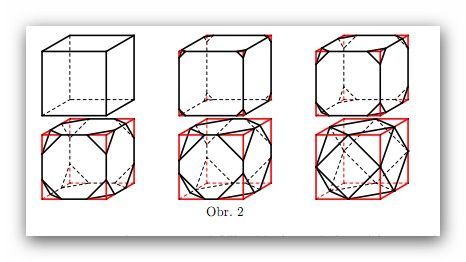
To vypadá strašidelně, ale ve skutečnosti je to jednoduché. Vyjdu opět z jednoho již zde užitého obrázku, který jsem uvedl u příkladu 3 (krychle ABCDEFGH); doplňte si tam středy hran a pro lepší dorozumění označte střed hrany EF jako M, hrany FG jako N a hrany FB jako O. Rovina MNO uřízne z krychle roh ve tvaru čtyřstěnu MNFO, totéž udělají roviny proložené těmi ostatnímu středy podle níže přiloženého obrázku (ten poslední v řadě).
Ten označený čtyřstěn mohu chápat jako trojboký jehlan se základnou MNF a s vrcholem O (možná by se vám víc libilo brád to jako jehlan se základnou MNO a vrcholem F; to taky jde, ale výpočet by se trovhu komplikoval). Objem tohoto jehlanu /čtuřstěnu) snadno spočtu (jedna třetina základna krát výška, výška je |FO| = 0,5 dm, základnový (pravoúhlý) trojúhelník má základnu MF a výšku FN, pbé o velikosti 0,5 dm), vynásobím osmi (počet uřezaných rohů) a odečtu od objemu krychle.
Příklad 10:
Stačí uvažovat třetinu plechovky s jedním míčkem, poměr bude stejný. Poloměr míčku budičž r, to bude i poloměr válce /třetiny plechovky), jeho výška bude 2r, a teď už stačí použít známé vzorce. Je to vlastně klasická úloha Archimedova náhrobku, viz
kde je také obrázek a dokonce úplné řešení.
0x
Tak teď od konce.
Příklad 13:
Čtverec PQRS je zřejmě polovinou čtverce ABCD, Hranol o základně PQRS a výšce rovné hraně krychle má objem základna krát výška, a protože základna je polovic základny krychle, i objem hranolu je polovina objemu krychle. Objem (čtyřbokého) jehlanu je jedna třetina základna krát výška, tedy třetina objemu hranolu. Je to tedy? objemu krychle? (Zde obrázek nepřipojuji, to snad opravdu není třeba.)
Příklad 12. Poloměr koule vepsané do krychle je poloviční hrana této krychle (obrázek viz Archimedův náhrobek.
Koule opsaná má střed ve středu krychle, prochází všemi vrcholy, ergo její poloměr je polovina tělesové úhlopříčky; tu vypočteme z Pythagorovy věty (obrázek festival.1september.ru/... vzorec aristoteles.cz/... - obecně pro kvádr).
Příklad 11
Šířka haly je průměr d toho válce, její délka je výška v téhož.. Dle zadání v = 8/3 r, to dosadíme pro vzorec pro plášť válce, porovnáme s dvojnásobkem zadaného obsahu střechy a vše vypočteme.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.