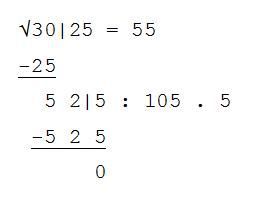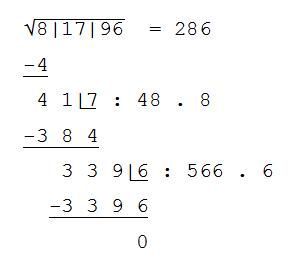Nejste přihlášen/a.
Chtěl bych se zeptat,jak určím odmocninu čísla 3025 bez pomoci kalkulačky?
2x
Pomocí tzv. částečného umocňování. Vysvětlím na příkladu:
Odmocnina z 500 = Odmocnina z (5*100)= odmocnina z (5*4*25), 25 a 4 lze odmocnit z hlavy, takže dostaneme = 2*5 odmocnin z 5. Takže výsledek je 10 domocnin z 5. ![]()
Stačí takto?
doplněno 28.03.11 19:06:Tak 3025 je taky dělitelné 25, to vidíte na posledním dvojčíslí. Takže 3025/25=121, takže v prvním kroku to bude odmocnina z 25*121. 25 odmocníme, tím ji dostaneme zpod té odmocniny, 121 tam zůstane - a máme 5 odmocnin ze 121... Tak zkuste, jestli to jde ještě něčím vydělit. ![]()
Ano, vyjde to 55. Protože 121 rozložíme jako 11*11. To je to samé jako 11 na druhou. Takže 121 odmocníme na jedenáctku, tím se dostane před odmocninu (pod kterou už nic nezůstane) a která se vynásobí s předem odmocněnou pětkou. Kapišto?
doplněno 28.03.11 19:25:.
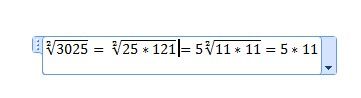
2x
Cifry daného čísla rozdělíme na skupiny po dvou počínajíc od základního místa. První skupina odleva je 30. Odhadneme: √ 30 je více než 5, ale méně než 6. Napíšeme 5 do výsledku a pod 30 uvedeme výsledek umocnění 52, tj. 25. Odečteme od 30, ke zbytku připíšeme další dvojčíslí, tj. 25 a oddělíme poslední cifru, tj. 5. Odhadneme podíl při dělení čísla 52 dvojnásobným dosud napsaným výsledkem, tj. 10 (=2 . 5). Tento podíl, tj. 5, uvedeme jako další cifru do výsledku, připíšeme za číslo, kterým dělíme (10) a znásobíme 105 . 5 =525 a odečteme. Podobně postupujeme dále. Když na konci výpočtu nevychází zbytek nula, je odmocnina číslo iracionální a výše popsaným způsobem lze určit libovolný počet desetinných míst.
√30|25 = 55
-25
5 2|5 : 105 . 5
-5 2 5
0
doplněno 28.03.11 19:49:Přikládám obrázek, zde se cifry posunuly, takže nejsou správně pod sebou. Celý postup připomíná písemné dělení, ale to již dnes žáci neumí.
2x
To jsou samé algoritmy a výpočty na stránku. Nešlo by to jem prostou úvahou, kdy 50x50 je 2500 a 60x60 je 3600. Tak výsledek bude v itervalu mezi těmito čísly. Výsledné číslo bude dělitelné 5 a tak vychází jen 55
V zásadě je to pravda, díky tomu, že ta odmocnina je celočíselná. Ty postupy jsou dobré na ovecný případ, ale otázka byla speciální. A protože kontrolou vyjde 55*55 = 3025, tak je to O.K.
Kdyby to nevyšlo, tak holt by nám ty algoritmy byly dobré, ale navíc i tentopostup lze vzít za základ algoritmu, zvaného metoda dělení intervalu. Když jsem zjistil, že odmocnina je mezi 50 a 60, tak rozdělím tento interval na půlku a zkusím; zde to vyjde přesně, ale kdybych odmocňoval třeba 3040, zjistil bych, že výsledek je mezi 55 a 60, tak bych zkusil třeba 57 (abych se aspoň pro začátek vyhnul zlomkům) a tak dále.
1x
Petapeta uvádí jeden algoritmus, je popsán taky v mfweb.wz.cz/.... Jeho výhoda je v tom, že počítá postupně všechna desetinná místa popořadě. Existuje i jiný algoritmus, v podstatě iterační, který se mi skoro líbí víc, i když nepostupuje po des. místech. Jeho myšlenka je tato: pro začátek odmocninu (označme ji a, tedy a2 = 3025) odhadu (čím přesněji, tím lépe, ale kouzlo je v tom, že na té přesnosti mc nezáleží) , a pak se pokusím vypočítat opravu. Na příkladě, třeba s tou 3025. První odhad označím a1 a nastřelím ho třeba a1 = 50 (nebo chcete-li, a1= 100 000, ale to by trvalo déle), a opravu, chybu, označím e1, takže a = (a1+ e1) a
a2 = 3025 = a12 + 2a1*e1 + e12
To je kvadratcká rovnice pro e1, ale to se mi nelíbí, tak si řeknu, že to e1 bude malá chyba (při té druhé volbe a1 = 100 000 moc malá nebude, ale kupodivu metoda funguje stejně, ovšem z jiného důvodu), takže e12 bude ještě menší a můžeme ho zanedbat. Dostaneme tedy rovnici
3025 ≈ a12 + 2a1*e1 , v našem případě 3025 ≈ 50*50 + 2*50*e1 , 3025 ≈ 2500 + 100e1
odkud vypočteme e1 ≈ 5,25, a ≈ 55,25 (ta dvouvlka znamená přibližnou rovnost).
To číslo 55,25 samozřejmě není přesně odmocnina, ale vezmu to jako první opravu. čili druhý, vylepšený odhad a označím ho a2.= 55,25. No a s tímto lepším odhadem postup zopakuji a = (a2 + e2), 3025 ≈ a22 + 2a2*e2
e2 ≈ (3025 - a22)/2a2 = (3025/2a2 -a2/2 ) (oba vzorce jsou správně, ale v tom prvním musíme umocňovat na druhou, čemuž se ve druhém vzorci vyhneme), s konkrétními čísly máme e2 ≈ 3025:110,5 – 55,25:2 = -0,25 (na dvě desetinná místa), a jako další odhad položíme a3 = 55 a hru opakujeme. V tomto případě ku podivu, právě díky zaokrouhlení, nám vyšl apřesná odmocnina; kdybych pošítal "přesnějí"na tři desetinná místa, dostal bych e2 = -0,249, a3 = 54,001 a ještě chvíli bych počítal.
Takže shrnu li algoritmus, bude to takto:
Počítám odmocninu z A, označenou a.
Krok 1: Zvolím jakkoli první aproximaci a1 a spočtu opravu e1 podle vzorce
e1 = A/2a1 - a1*/2; za druhou aproximaci a2 vezmu a1+ e1
2, Iterační krok: Mám-li spočtenu i-tou aproximaci ai, spočtu (i+1)tou aproximaci ze vzorce a(i+1) = ai + ei. kde
ei = A/2ai - ai/2
3. Tento postup opakuji tak dlouho, dokud oprava ei nebude dostatečně malá. Chci-li například počítat na pět desetinných míst, budu pracovat tak dlouho, dokud b nebude mít na prvních pěti des. místech nuly.
doplněno 29.03.11 13:18:
V popisu algoritmu u kroku 1 se mi připletla hvězdička; má to být takto:
==================================================
Krok 1: Zvolím jakkoli první aproximaci a1 a spočtu opravu e1 podle vzorce
e1 = A/2a1 - a1/2; za druhou aproximaci a2 vezmu a1+ e1
====================================
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.