Nejste přihlášen/a.
0x
Zdravím,
tady je odkaz na teorii
Příklad 44 :
Je to příklad na kombinace druhé třídy z n prvků. Kombinace druhé třídy je to proto, protože konkrétní průsečík je průsečík protnutí právě dvou konkrétních různoběžek.
C2 (n) = 55
n je počet těch různoběžek
n krát (n-1) : 2 = 55
n krát (n-1) = 110
n2 - n = 110
n2 - n - 110 = 0
Řešením této kvadratické rovnice jsou čísla 11 a - 10
Řešením příkladu je číslo 11.
doplněno 28.12.24 12:19:
Poznámka:
Dle Vaších zápisků je pro označení kombinace používáno písmeno K.
Já pro označení kombinace používám písmeno C.
doplněno 28.12.24 12:23:
Poznámka:
Označení kombinace v textu toho souboru
Ck (n)
je stejné označení, jako označení
K (k, n)
0x
Ahoj,
posílám 46+47, z toho můžeš usoudit na 45+48.
O správnosti zápisu se lze přesvědčit vyřešením příkladu.
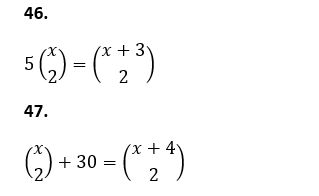
0x
Příklad 45:
K (k, n) = K (k, n - 4)
Jedná se o kombinace druhé třídy, takže za k dosadíme 2
K (2, n) = 3 krát K (2, n-4)
Použijeme opět vzorec pro kombinaci
n krát (n-1) : 2 = 3 krát (n-4) krát (n-5) : 2
n krát (n-1) = 3 krát (n-4) krát (n-5)
n2 - n = 3 krát (n2 - 5n - 4n + 20)
n2 - n = 3 krát (n2 - 9n + 20)
n2 - n = 3 n2 - 27n + 60
0 = 2 n2 - 26n + 60
0 = n2 - 13n + 30
Řešením této kvadratické rovnice jsou čísla 3 a 10
Řešením příkladu je číslo 10
Dá se to ověřit na kalkulačce. Kombinace jsou na kalkulačce počítány použitím funkce nCr
10 nCr 2 = 45
6 nCr 2 = 15
Poznámka:
Výsledek je 10 , protože otázka v zadání úlohy je to, vypočítat, jak velké je číslo, které je zmenšeno.
Zmenšeno je číslo 10 a po zmenšení se to číslo zmenšilo na 6.
0x
Př. 49:
V tomto příkladě je použito tzv. kombinatorické pravidlo součinu, viz. např.
Z množiny početu chlapců vybíráme 2 chlapce. Proto použijeme kombinaci druhé třídy.
Z množiny počtu děvčat vybíráme jednu dívku. Proto použijeme kombinaci první třídy.
K (2, 13) krát K (1, 15) = 78 krát 15 = 1170
Př. 48
Původní počet prvků je n
Počet prvků po zmenšení je n - 5
K (2, n) - 25 = K (2, n - 5)
K (2, n) = K (2, n - 5) + 25
n krát (n - 1) : 2 = (n - 5) krát (n - 6) : 2 + 25
Rovnici vynásobíme krát 2
n krát (n - 1) = (n - 5) krát (n - 6) + 50
n2 - n = n2 - 6n - 5n + 30 + 50
Z obou stran rovnice odečteme n2 takže v tomto řešení nevzniká kvadratická rovnice
- n = - 6n - 5n + 30 + 50
10 n = 80
n = 8
Kontrola na kalkulačce je:
8 nCr 2 = 28
3 nCr 2 = 3
Př.47
Tento příklad je principielně podobný jako př. 48
Původní počet prvků je n
Počet prvků po zvětšení je n +4
K (2, n) + 30 = K (2, n + 4)
n krát (n - 1) : 2 + 30= (n + 4) krát (n + 3) : 2
Rovnici vynásobíme krát 2
n krát (n - 1) + 60 = (n + 4) krát (n + 3)
n2 - n + 60= n2 + 3n + 4n + 12
Z obou stran rovnice odečteme n2 takže v tomto řešení nevzniká kvadratická rovnice
- n + 60 = 3n + 4n + 12
- 8n = - 48
n = 6
Původní počet prvků byl 6
Po zvětšení byl počet prvků 10
10 nCr 2 = 45
6 nCr 2 = 15
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.
