2x
Čísla ti tam asi sedí.
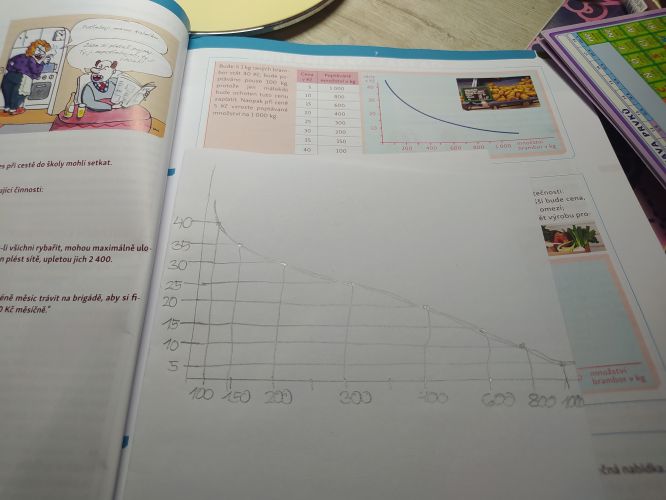
Ale vyfocené je to z blbého úhlu a ten graf má spoustu chyb
Stupnice nezačínají nulou a i když se tváří jako lineární tak nejsou, takže ta křivka nad nimi je sice klesající, ale její tvar nic nevypodá, ačkoli by měl.
Od začátku ke stovce (interval 100) je míň než od 100 ke 150 (interval 50), 100-200 je menší než 300-400 a větší než 800-1000 atd.
Křivka sahá i mimo zadané hodnoty.
Takže při rýsování tam tu nulu vyznačte pro obě osy, dodržte stejnoměrné vzdálenosti a křivku vyneste jen tam, kde ty hodnoty máte. Pokud bude vypadat nějak rozumně (třeba jako hyperbola), tak můžete pokračování naznačit čerchovaně/přerušovaně jako hypotetickou extrapolaci
Já bych extrapolaci osobně nedělal, pokud to zadání úkolu nevyžaduje, zejména ne u takových věcí jako je poptávka, kde to na krajích začnou výrazně ovlivňovat jiné vlivy - při nulové ceně se neprodá nekonečné množství, protože jednak prostě tolik brambor nebude a naopak ani zdarma nikdo nekoupí tunu brambor, když ji nebude mít kam dát ani jak odvézt. A na druhé straně od určité ceny ten graf nebude dávat smysl, protože se brambory neprodávají po gramech, nebo miligramech.
Monotónní aproximace s nejnižší chybou je v tomto případě podle kalkulátorů logaritmická aproximace typu a - b.log(x)
Hyperbolická je naopak zdaleka nejhorší. 
Já jsem tu neřešil ta čísla, hyperbola byl první zaoblený tvar, co mě napadnul. V tom náčrtku to vypadá na dvojnásobně zalomený luk. Taky jsem si až teď všimnul, že tam obrázek už je.
Ale podle znění mi to přišlo jako typický učebnicový příklad, kde jsou náhodná čísla a ta slova okolo jsou jen omáčka, aby to pro děti bylo zajímavější. Jako v té učebnici, co o ní psal Feynmann, kde si zavedly teplotu hvězd podle barvy, on se napružil už u první hodnoty, která byla zcela mimo obvyklý rozsah, u hvězd fialových a zelených už vypěnil ale vrchol byl, když vlastní úloha byla, kolik jakých hvězd které dítě vidí a měla se spočítat celková teplota.
Počítat, kolik se brambor prodá při jaké ceně od 5 do 40 korun a dělat závěry na 1-10 stovkách kilo, je stejně už na první pohled dost divná metodika.
Ten můj přříspěvek bylo jen takové pošťouchnutí. Uváděl jsem to čistě jako zajímavost. Běžně se totiž pokles poptávky popisuje jako "nepřímá úměra" (tj. hyperbola) a přitom při těchto datech by to byl logaritmický pokles.
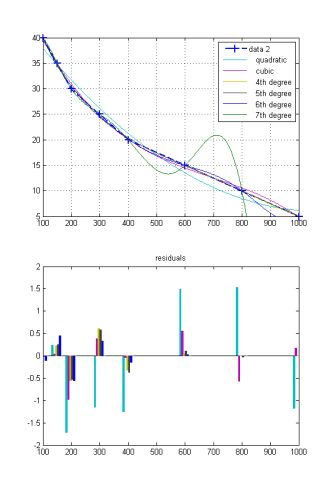
Úplně nejlépe z těch aproximací ale stejně s přehledem vyšla kubická. Jenže polynomiální aproximace (vyšších řádů) mají své známé problémy.
Kubická a další polynomy vychází divně. Ty polynomy se sice trefí do bodů, kubická je míjí. Bohužel tak jednoduchým způsobem neudělám ani logaritmus ani hyperbolu (tohle je co nabízí základní nástroj).
Kubická ji míjí, protože je třetího řádu a ty máš 8 bodů, tj. 8 rovnic pro (3+1) neznámé. Kubická tak může jen minimalizovat chybu a proto to je aproximace.
Další funkce si můžeš zkusit tady. Zkus si vypnout tu hyperbolu, která zbytečně smrskává osu y tím, jak vystřeluje k nekonečnu pro hodnoty x pod 100.
> polynomiální aproximace (vyšších řádů) mají své známé problémy
Je to krásně vidět v grafu od @mll, kde se polynom 7.řádu mezi 400 a 800 splaší a vrací úplné blbosti.
0x
Možná jsem to špatně pochopil, ale není ten graf celý blbě? Pokud má znázorňovat - čím vyšší cena, tím menší poptávka, nebylo by teda lepší kdyby hodnoty 100-1000 byli v levém sloupci a hodnoty 5-40 v tom spodním?
Jde o to, k čemu ten graf budeme chtít převážně používat a jak. (Ale tohle je nejspíš jen z prstu vycucaný příklad na kreslení grafu, bez vazby na realitu, takže je to fuk.)
Kdyby to mělo být k něčemu dobré, tak spíš k tomu, že mám malý omezený trh, kde se víc jak tuna brambor neprodá (třeba vesnice, malý krámek s dalšími v okolí a tak), ale já jich nemám celou tunu a tak chci vědět, jakou cenu mám nasadit, aby se to všechno prodalo a přitom jsem co nejvíc vydělal.
0x
Stupnice vodorovné osy (x) je trochu zvláštní. Jako pokus o logarotmickou stupnici (na začátku řídká, pak hustá).
A jinak bych řekl, že snad i prase by to namalovalo líp, i když nic ve zlém. Osy dejme tomu. Graf je tak nějak dvojmo. Ty pomocné čáry by mohly být tenčí. Jak značit body, já bych preferoval křížek.
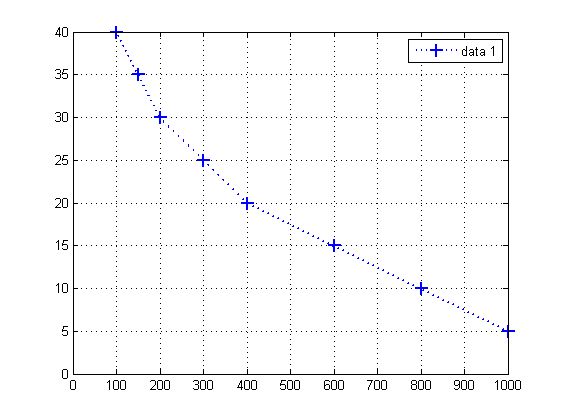
Když si tak zkouším ta čísla dát do grafu, tak mě vychází cosi divného, co hyperbolu moc nepřipomíná a veškeré pokusy o proložení čehokoliv selhávají. Takže tvar toho proložení bych asi tak neřešil (pokud jsem neopsal čísla blbě). Ale dát si ta čísla do excelu, nebo co vy mladí na těch mobilech máte je otázka na 2 minuty, takže udělat si představu o tvaru grafu je jednoduché. Pro mě je rychlejší dát to do Matlabu.
x=5:5:40
y=[1000 800 600 400 300 200 150 100]
plot(y,x,--+)
grid on
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.