Nejste přihlášen/a.
Ahoj, potřeboval bych poradit. Sedím nad tím už dlouho a nevím si s tím rady. Za případné opovědi nebo tipy moc děkuji.
Vypočtěte objem koule, která lze opsat rotačnímu kuželu o poloměru podstavy r a
výšce v.
2x
Z tveho blekotani neni prilis jasne, zda ma jit o kouli opsanou okolo kuzele nebo vepsanou v kuzelu, ale at uz tak nebo tak, nejde o nic jineho, nez o trojrozmerny pripad zakladniho dvojrozmerneho ukolu kruznice vepsane nebo opsane trojuhelniku.
Kdy kruznice je plosny rez stredem koule, trojuhelnik je plosny rez osou kuzele.
Jednoduchy vzorecek pro oba pripady (opsanost nebo vepsanost) lze snadno dohledat. Treba na wikipedii.
Takto ziskas polomer kruznice (opsane, nebo vepsane)
Objem koule se jiz pak spocte z polomeru kruznice pomoci vzorce pro objem koule.
0x
Nakreslite si priecny rez, bude tam pravouhly trojuholnik, rotaciou ktoreho okolo jednej strany vznikne kuzel, vnutri trojuholnika je polkruznica, ktora sa dotyka jeho prepony. Staci vypocitat polomer gule, objem je potom dosadenie do vzorca.
Dobrý den, já potřebuji ale udělat kružnici opsanou tomu kuželu a také bohužel nemám žádné číslené hodnoty. To zadání tak, jak ho píšu v první otázce je kompletní. Bohužel jsem moc nepochopil, jak mi pomůže sestrojení bočního řezu.
No přece se dá, když ti radí... viz
Střed kružnice opsané trojúhelníku je průsečík os stran trojúhelníku, poloměr se rovná vzdálenosti středu od libovolného vrcholu. Každému trojúhelníku lze opsat kružnici.
Skvěle, tohle jsem pochopil, ale ja kto mám spočítat, když nemám zadané žádné hodnoty? Předpokládám že bez nich poze dosazováním různých vzorečků do sebe. Nevím, jak mám tohle provést
Ano, vasa uloha je napisat vzorec pre objem gule, ked su zname vyska a polomer zakladne kuzela. Rovnako, ako napriklad objem kvadra V = a * b * c , teda sucin dlzok jeho hran.
V prvom kole najdete vzorec pre polomer gule, ako zavisi na "v" a "r" kuzela, nazvime ten polomer gule napr "rg", potom to len dosadite do vzorca pre V = 4 / 3 * pi * rg3
Udělal jsem v původním výpočtu chybu, tak tedy ještě jednou: ![]()
Z toho, co zde již bylo řečeno (střed S opsané kružnice na průsečíku stran) to jde dopočítat.
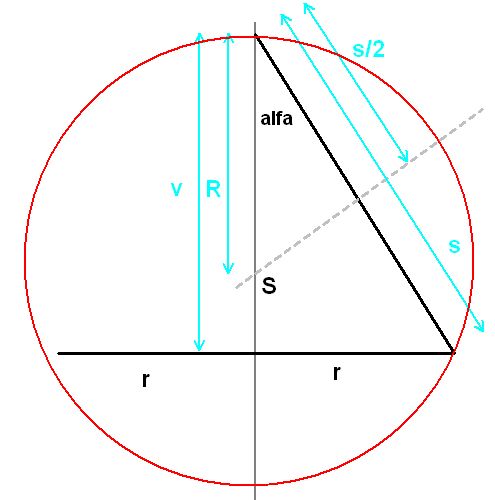
Středem spodní strany je rovnou osa rotace (je to rovnoramenný trojúh.). Hledáme proto jen střed jednoho ramena a jeho průnik s osou rotace, respektive vzdálenost toho průsečíku od jednoho z vrcholů (na obrázku R). To je pak i poloměr opsané kružnice a poloměr opsané koule rotačnímu trojúhelniku.
s = √ (r2 + v2)
Ze vzniklého pravoúhlého trojúhelníku u horního vrcholu:
cos(alfa) = (s/2) / R
Zároveň z celé pravé poloviny původního trojúhelníku:
cos(alfa) = v / s
neboli
v / s = (s/2) / R
R = s2 / 2v
R = s2 / (2v)
R= (r2 + v2) / (2v)
Objem opsané koule je tedy:
V = (4/3).π.R3
V = (4/3).π.(r2 + v2)3 / (23v3)
V = π.(r2 + v2)3 / (3.2.v3)
V = (π/6) . [(r2 + v2) / v]3
V = (π/6) . (r2/v + v)3
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.