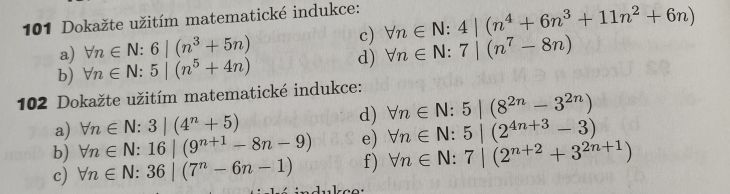0x
Je potřeba dokázat to pro 1, 2, 3 a hlavně pro n+1. Teda stačí pro 1 a n+1. A pokud to platí pro 1 a n+1 tak to platí pro jakékoliv přirozené číslo, protože tím jsou pokrytá všechna přirozená čísla. To je princip matematické indukce.
101/a
Máš dokázat, že výraz n^3 + 5n je dělitelný 6.
1. pro N=1 je výraz 1 + 5*1 = 6, což je dělitelné 6
2. Předpokládáš, že to platí pro n.
3. Pak by to mělo platit i pro n+1. Dosadíš tedy do daného výrazu (n+1)^3 + 5*(n+1).
Umocníš to, dáš stejné mocniny n k sobě.
4. Pokud je tento výraz dělitelný 6 a je dělitelný 6 i výraz pro n, musí být dělitelný 6 i jejich rozdíl. Uděláš tedy rozdíl těchto dvou výrazů a zůstane ti 3n^2 + 3n + 6, který máš dokázat, že je dělitelný 6. Pro sudá čísla je to triviální, pro lichá to dokaž sám.
Třeba to jde elegantněji.
0x
101 d
Dokazete to pre n = 1 dosadenim
Potom vyjdete z predpokladu, ze n^7 - 8n je delitelne 7 a ideme dokazat, ze to plati aj pre n + 1
Prepiseme si to na x ^ 7 - 8x a za x dosadime n + 1
Po umocneni tam bude plno clenov, ktorych binomicky koeficient bude napr 21 alebo 35, co ju svetko cisla delitelne 7
Ked ich odtial vyhodite prec, ostane vam povodnych n ^ 7 - 8n, ktore podla predpokladu su 7 delitelne, cim je to cele dokazane.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.