Nejste přihlášen/a.
a=7 cm,b=6cm,S=60cm2.
0x
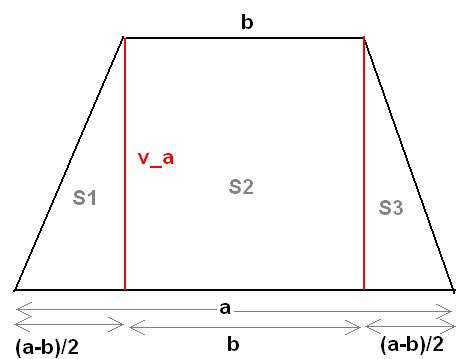
S = S1 + S2 + S3
S = (1/2).[(a-b)/2].va + b.va + (1/2).[(a-b)/2].va
S = [(a-b)/2].va + b.va
S = va.[(a-b)/2 + b]
S = va.[(a-b+2b)/2]
S = va.(a+b)/2
S = [(a+b)/2] . va ⇒ známý vzorec
va = 2.S/(a+b)
va = 2.60/(7+6)
va = 9,23 cm
doplněno 10.06.24 04:47:
@kmet má tedy výsledek správně, jen ho napsal pozadu ![]()
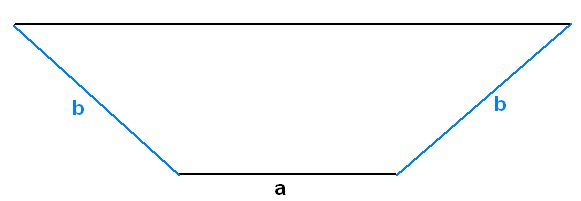
Zdravím a dovoluji si uvést svůj názor: Pokud je v zadání a základna tohoto lichoběžníka, pak strana b je jeho rameno a druhá základna (potřebná při výpočtu obsahu) je c. Ta je bohužel neznámá...
> strana b je jeho rameno
Fuj, to byl ošklivý chyták! Až se stydím přiznat, že jsem nad řešením strávil mnohem více času, než bych měl. ![]()
![]()
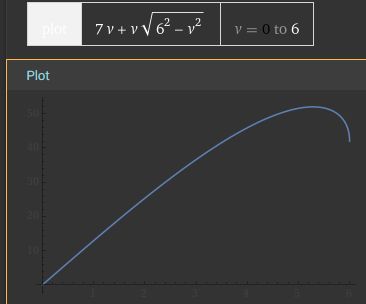
Řešení: Kdyby strany b trčely kolmo nahoru, tak z lichoběžníka je běžný obdelník o obsahu 6.7 = 42, tedy méně než požadovaných 60. Naklápěním stran směrem dovnitř obsah lichoběžníku jen zmenšuje, takže strany musíme vyklápět směrem ven (viz obr.). Tím přidáváme obsah v postranních částech. Zároveň se nám ale začne snižovat výška a tedy ubývat obsahu v té střední obdelníkové části.
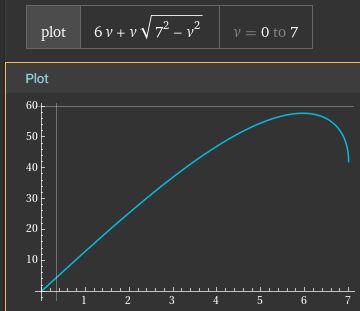
Když si vyjádříme obsah lichoběžníku jako funkci výšky, vyjde nám polynom 4.řádu. Po vykreslení grafu funkce vidíme, že obsah pro žádnou výšku nikdy nedosáhne hodnoty 60. Maximálního obsahu lichoběžník dosáhne kolem výšky asi 6 cm a to asi 58 cm2.
> vyjde nám polynom 4.řádu
Oprava: není to polynom. Popletl jsem to tady s mým mezivýpočtem v jednom ze svých pokusů o řešení ![]()
> Maximálního obsahu lichoběžník dosáhne kolem výšky asi 6 cm a to asi 58 cm2
Kdyby někoho zajímaly přesné hodnoty:
5,9595403051898978414218341270002
57,640913503019453581213005156594
Zdravím a potvrzuji, že takový rovnoramenný lichoběžník (obsah 60, základna 7, rameno 6) neexistuje...
- Obsah lichoběžníku
- Jak vypočítat obsah tohoto lichoběžníku
- Obsah lichoběžníku
- Obsah lichoběžníku
- Potřebuji poradit s příklady
- Jak vypočítat obsah lichoběžníku
- Vyučují se ve škole nesmysly?
- Těžiště plochy
- Vypočítej obsah lichoběžníku
- Slovní úloha
- Příklady na vypočítání
- Výpočty příkladů
- Obdélník, lichoběžník
- otázka , jak vypočítat lichoběžník
- Příklady z goniometrie
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.