Průsečík s osou x a nulové body funkce

> jak by se daly v rovnici naleznout nulové body?

To je podle mě netriviální problém řešitelný snad jedině přes Lambertovu W funkci.

> jak [...] dokázat, že rovnice y= 2x² - lnx nemá žádný průsečík s osou x?

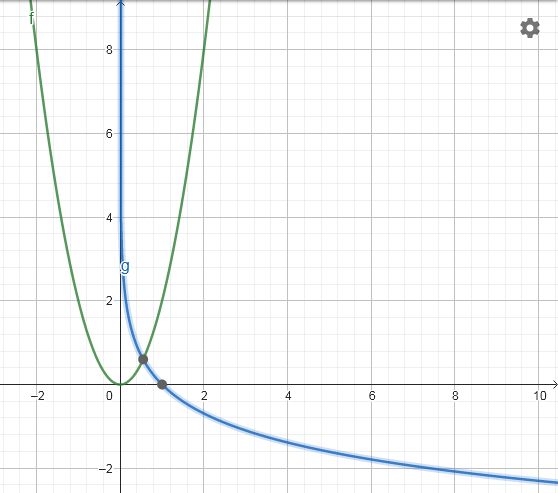
Sám bych to ukázal na grafech funkcí.

Řešil bych to jako y = 2x² + (-ln(x)).

Z grafu je vidět, že v <0,1> sčítáš 2 kladná čísla a výsledek bude kladný a pro x>1 rostě 2x² mnohem rychleji než ln(x) klesá.

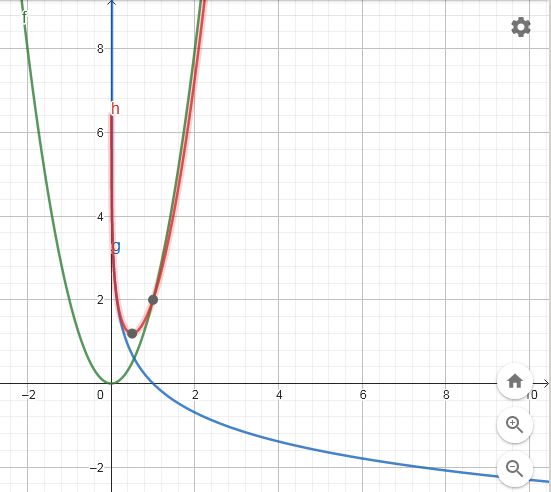
Na druhém grafu je vidět jejich červený součet.

Předpokládám, že jde o rovnici y=2x² - ln(x) pro x>0

Jeví se mi jasné, že x² je pro x>0 kladné, ln(x) pro x<1 je záporné, kladné číslo minus záporné číslo je samozřejmě kladné.

pro x=1 je 2x² - ln(x) rovno 2-0 = 2 tedy kladné

pro x>1 je derivace(2x² - ln(x)) = 4x-1/x a 4x je zde vždy větší než jedna, zatímco 1/x je menší než jedna, jejich rozdíl je tedy kladný a původní funce je tedy rostoucí. Funkce rostoucí od 4 výše je pochopitelně také kladná.

Funkce, která je všude kladná pochopitelně nemá průsečík s osou x.

Což bylo dokázati.

(Určitě jsou i jiné postupy, tohle je první, co mě napadlo)

Další možnost výpočtu naznačil už trochu @kdosi.

Najdeš minimum funkce (derivací), spočítáš v minimu funkční hodnotu a když je tato hodnota kladná, tak funkce pod 0 vůbec nespadne.

df = 4x - 1/x = 0

4x² = 1

x = 1/2

y" = d²f = 4 + 1/x²

y"(1/2) = 4 + 4 > 0 ⇒ globální minimum

f(1/2) = 2.(1/4) - ln(1/2) = 1/2 + ln(2) > 0 ⇒ Funkce vůbec neklesne pod osu x.