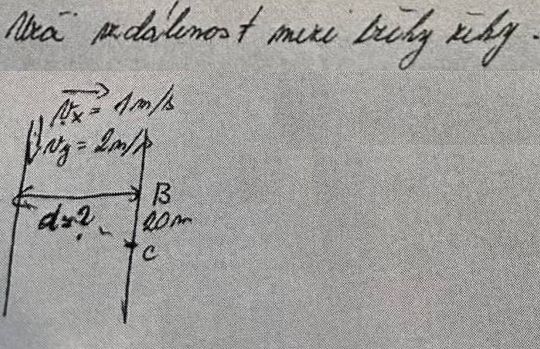0x
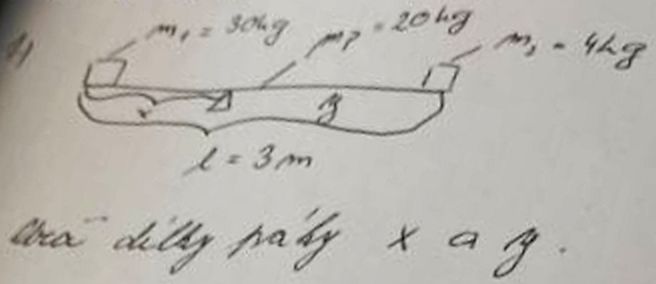
Př. č.1:
Levá část tyče váží (x/l).mp
Pro uvažování, jaký je její moment síly na páce, ji místo působení celé váhy (polo)tyče podél délky x nahradíme stejně těžkým hmotným bodem v polovině ramene páky: M = F.r = F.(x/2) = m.g.(x/2) = (x/l).mp.g.(x/2)
Obdobně pro pravou část tyče: M = (y/l).mp.g.(y/2) = [(l-x)/l].mp.g.[(l-x)/2]
Celkové momenty sil na páce:
m1.g.x + (x/l).mp.g.(x/2) = m2.g.(l-x) + [(l-x)/l].mp.g.[(l-x)/2]
vykrátit g a dosadit:
30x + (x/3).20.(x/2) = 4.(3-x) + [(3-x)/3].20.[(3-x)/2]
30x + (10/3)x2 = 12 - 4x + (10/3).(9 - 6x + x2)
34x + 20x = 12 + 30
x = 7/9 = 0,777 m
y = l - x = 3 - 0,777 = 2,222 m
Snad jsem někde neudělal chybu.
0x
Př. č.2:
Zadání jsem nepochopil. ![]()
doplněno 22.03.24 07:12:
Jestli to v2 je boční vítr, pak vzdálenost AB i AC uletí za t=s/v1 = 600/300 = 2 h, ale protože je tam ta složka v2 , tak místo v B skončí v C a to v2 ho za ty 2h odfoukne o s = BC = v2.t = 72.2 = 144 km, takže z C musí letět proti větru do B a jeho celková rychlost bude 300-72 = 228 km/h a těch 144 km z C do B uletí za tCB = s/(v1-v2) = 144/(300-72) = 0,63 h, takže celkem let ACB bude trvat 2 h + 0,63 h = 2,63 h = 2h 37m 54s.
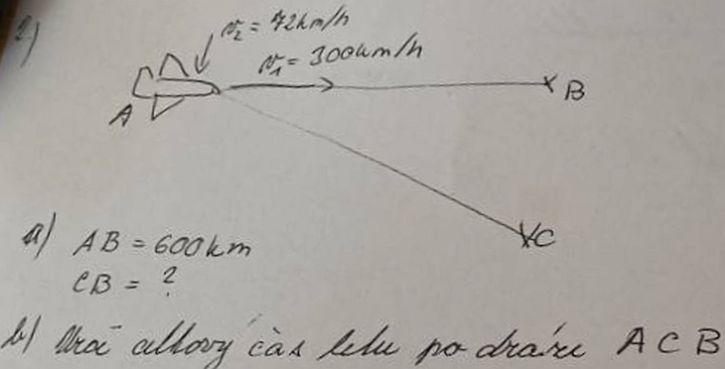
0x
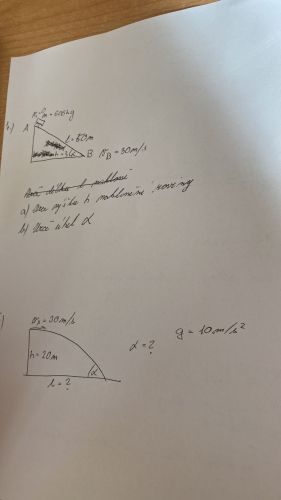
Př. č.3:
Zákon zachování hybnosti.
Jen červená složka rychlosti působí ve směru nového pohybu.
Po dopadu kámen zůstane ve vozíku a tedy celková hmotnost soustavy je m+mv.
Žluté úhly jsou všechny α.
m.v1x = (m+mv).v
m.v1.sin(α ) = (m+mv).v
v = [m/(m+mv)] . v1 . sin(α )
v = [10/(10+80)].40.sin(45)
v = 3,1 m/s
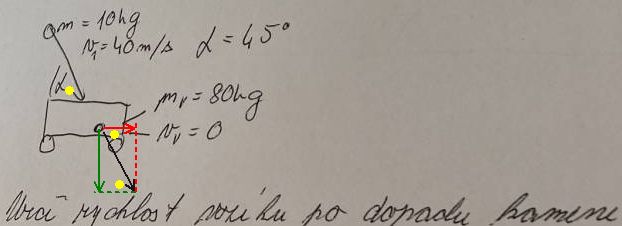
0x
Př. č.4:
Pohyb rovnoměrně zrychlený.
Jen červená složka černé tíhové síly Fg působí ve směru pohybu vozíku.
Žluté úhly jsou α.
Předpokládám m=606 kg. Jestli je to 600 kg, tak si to musíš přepočítat.
F = m.a
Fg.sin(α ) = m.a
m.g.(h/l) = m.a
a = g.(h/l)
------
v = a.t = g.(h/l).t
t = v.(l/h)/g
------
s = l = (1/2).a.t2
l = (1/2).g.(h/l).v2.(l/h)2/g2
l = (1/2).v2.(l/h)/g
h = v2/(2g) ; Fuj, to je dlouhý výpočet na odvození známého vzorce v = √ (2hg) !
h = 302/(2.9,8)
h = 45,9 m
--------
sin(α ) = h/l
sin(α ) = 45,9/50
α = 66,7°
-------
Aha, ono to na váze vozíku nezávisí, protože v gravitačním poli se tělesa pohybují se stejným zrychlením. ![]()
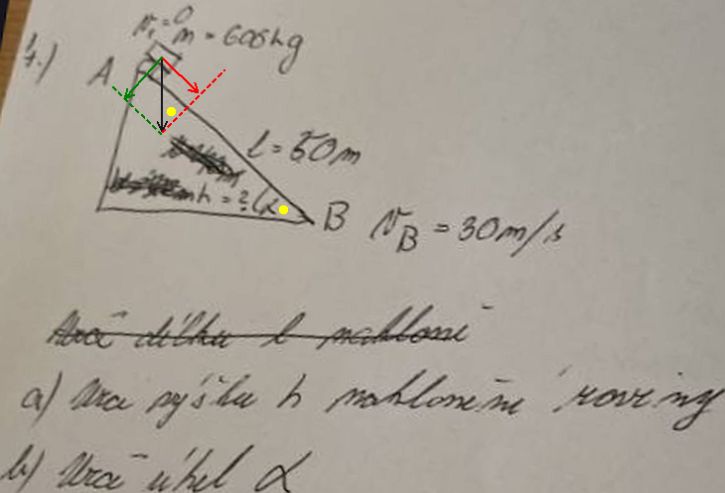
0x
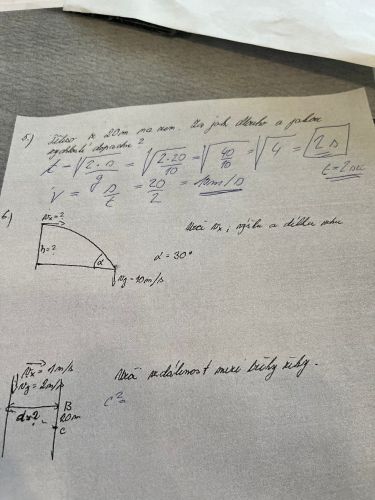
Př. č.5:
Z výšky h těleso spadne za dobu t bez ohledu na to, nakolik se pohybuje ve směru osy x:
s = h = (1/2).g.t2
t = √ (2h/g)
t = √ (2.20/10) = 2 s
Těleso dopadá (zelenou) rychlostí:
vy = g.t = 10.2 = 20 m/s
Za 2 sekundy uletí ve směru x dráhu:
l = vx.t = 30.2 = 60 m
-----------
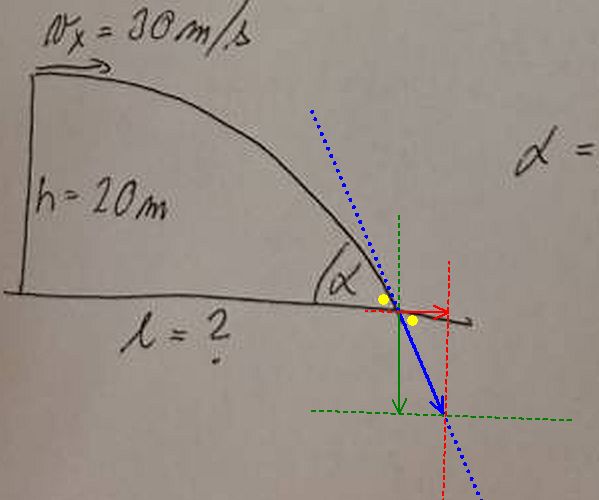
Úhel α je v okamžiku dopadu stejný jako vektor okamžité (modré) rychlosti, který je dán jeho vodorovnou (červenou) složkou vx a svislou (zelenou) složkou vy:
Žluté úhly jsou stejné.
tg(α ) = vx/vy
tg(α ) = 30/20
α = 56°
doplněno 22.03.24 05:35:
Lepší obrázek, že vektor okamžité (modré) rychlosti v momentu dopadu je tečna ke křivce pádu v tomto bodě a že úhel dopadu jde vyjádřit jako funkce vx a vy.
Tímto větším rozkreslením také zjišťuji, že jsem ten úhel α na původním obrázku označil chybně a důsledkem toho ho i počítal blbě. ![]() Správně má být poměr opačně:
Správně má být poměr opačně:
tg(α ) = vy/vx = 20/30
α = 33,7°
Měl jsem si chyby všimnout hned, když jsem měl vx > vy, tak mi nemůže vyjít úhel větší než 45°!
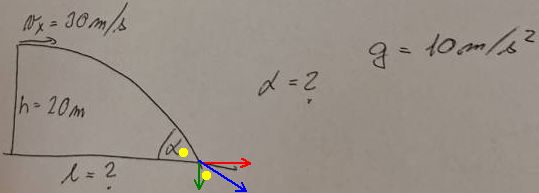
0x
Př. č.6:
g = 10 m/s2
vy = g.t
t = vy/g = 10/10 = 1 s
h = (1/2).g.t2 = (1/2).10.12 = 5 m
tg(α ) = vx/vy ; viz příklad č.5
vx = vy.tg(α ) = 10.tg(30) = 5,77 m/s
l = vx.t = 5,77.1 = 5,77 m
doplněno 22.03.24 05:41:
OPRAVA!
Jak je vysvětleno pod příkladem č.5, výpočet α je špatně. ![]() Správně má být poměr opačně:
Správně má být poměr opačně:
tg(α ) = vy/vx
vx = vy/tg(α ) = 10/tg(30) = 17,3 m/s
l = vx.t = 17,3.1 = 17,3 m
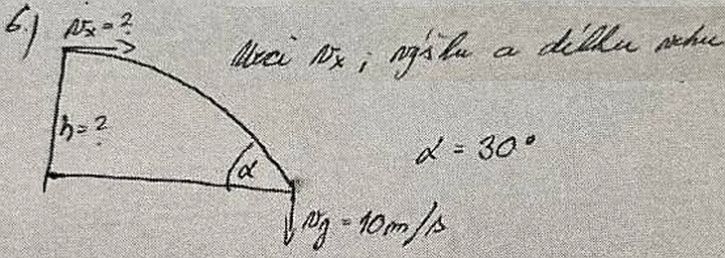
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.