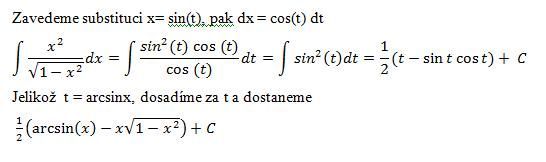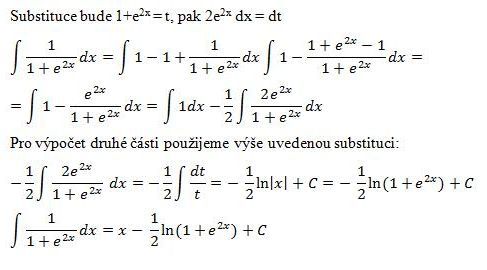Nejste přihlášen/a.
nevím si rady s příkladama, který jsou červeně zakroužkovaný.viz obrázek pomuže někdo spočítat?:/
děkuju moooc![]()

1x
1) integral x^3/(2+sqrt(4-x^2)) dx = x^2+1/3 (4-x^2)^(3/2)+constant
2) integral x sin^(-1)(x) dx = 1/4 (sqrt(1-x^2) x+(2 x^2-1) sin^(-1)(x))+constant
5) integral (sin(x))/(9+cos^2(x)) dx = -1/3 tan^(-1)((cos(x))/3)+constant
6) integral (cos(x))/(cos(x)-1) dx = x+cot(x/2)+constant
7) integral 1/(1+exp(2 x)) dx = x-1/2 log(e^(2 x)+1)+constant
8) integral (1+ln(x+1))/(x+1) dx = 1/2 ln(x+1) (ln(x+1)+2)+constant
nevím jak dál. viz obrázek nevím si rady s upravou![]()
po substituci a per partes mi vysli tyhle integraly a nevim si rady s dalsi upravou j

U toho prvního přepíšu integrand do tvaru (1/9)(1/(1+(t/3)^2), zasubstituuji t/3 =u a nakonec vyjde orkustangenta u (něčím vydásobená)
druhý upravím na parciální zlomky, tj na tvar (at+b)/(1+t^2) + c/t a na první část nakonec použiju podobný trik jako v předchozím příkladě
v tom třetím ještě položím t = u^2 a převedu na integráo z racionální funkce (zase parciální zlomky, i když tady v jednoduché podobě a po částečném vydělení jmenovatelem)
no a v tom posledním bude nejjednodušší goniometrická substituce jaku v prvním,
zatím postupuju takto,ale tady ty 3 příklady dál nevím:/
doplněno 09.03.11 21:12:poprvé se mi nevložil obrázek

0x
No to jde různě. Poradím začátek, ale to ještě není úplné řešení, bude to chtít další úpravy.
Příklad 1: začal bych substitucí x = 2 sin t (pokračovalo by to asi substitucí cos t = z) nebo (2-x)/(2+x) = z
Příklad 2 - per partes (x integruji, arcsin x derivuji)
př.5 je jednoducý - substituce cos x = t, - sin x dx = dt
př. 6 - zkus tg x = t
př. 7 - e^(2x) = t
př. 8 ln (x+1) = z (a tedy dx/(x+1) = dz)
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.