Záhada kombinace párů členů týmu

Tady máš jeden možný scénář

01-23-45-67-89-
02-13-46-58-79-
03-12-47-59-68-
04-15-26-39-78-
05-14-27-38-69-
06-17-28-35-49-
07-18-29-34-56-
08-19-24-36-57-
09-16-25-37-48-

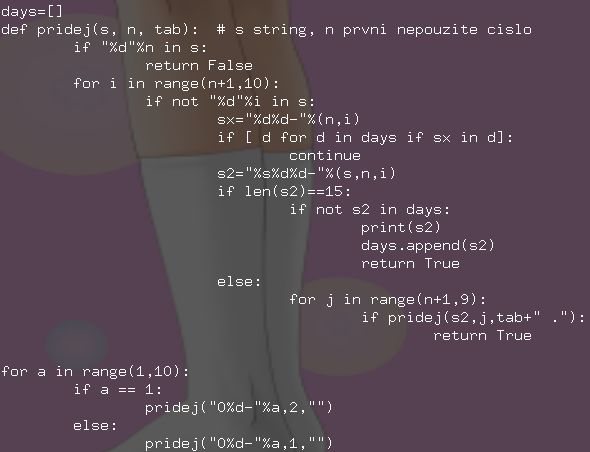
a tady program, který ho vypočítal

#!/usr/bin/python -u
days=[]
def pridej(s, n, tab): # s string, n prvni nepouzite cislo
if "%d"%n in s:
return False
for i in range(n+1,10):
if not "%d"%i in s:
sx="%d%d-"%(n,i)
if [ d for d in days if sx in d]:
continue
s2="%s%d%d-"%(s,n,i)
if len(s2)==15:
if not s2 in days:
print(s2)
days.append(s2)
return True
else:
for j in range(n+1,9):
if pridej(s2,j,tab+" ."):
return True

for a in range(1,10):
if a == 1:
pridej("0%d-"%a,2,"")
else:
pridej("0%d-"%a,1,"")

*********************************

Jak se tu udělá kód, mě to vyházelo všechna odsazení, což v pythonu celkem vadí ...

lidi značím číslovkama "0"-"9" protože se mi tak snadno procházejí

Bez Újmy Na Obecnosti (=BÚNO) jde při zápisu lidi ve dvojicích mít seřazené vzestupně (je fuk, jak v té dvojici stojí, takhle je snadno můžu hledat)

BÚNO jde mít dvojice seřazené podle numerické hodnoty

dvojice zapisuju s oddělovačem, takže při hledání v řetezci 01-23-45-67-89- mi to (správně) nenajde dvojici 12

Důsledek je, každý řetězec začíná dvojící "0"něco a druhá dvojice začíná buď 1, nebo pokud něco byla 1, tak začíná 2

Odsazení je v pythonu úroveň vnoření, stejně jako v C to jsou { ... } a v Pascalu begin ... end

days je list, kam dávám už nalezené dny. Používám ho abych zkontroloval, že dvojice nebyla ještě použitá. Mohl bych ho na konci vypsat, ale ladilo se mi to líp s průběžným vypisováním a pak už je to zbytečné opakovat

pridej je funkce, která k rozpracovanému řetězci přidává další dvojice

první parametr s je uvažovaný řetězec, druhý n je číslo, od kterého se mají zařít hledat nové dvojice. Třetí parametr (tab) není potřeba, používal jsem ho při ladění pro odsazování tisku

pridej projde možné kandidáty na další dvojici ("n"něco) a pro každého slibného se zavolá znovu pro doplnění řetězce s tímto kandidátem (s2)

něco musí být větší než n, protože tak je řadím

Pokud najdu vhodný řetězec o délce 15 (5 dvojic s oddělovači), tak ho vypíšu, přidám k days, vrátím True a končím včetně všech volajících, protože řetezec se stejnou první dvojicí už by znamenal opakování, takže není potřeba dál zkoumat tuto větev

Pokud je n už obsaženo v řetězci s, tak pridej končí hned, protože by se ten člověk jinak počítal dvakrát. Je to jednodušší testovat v té funkci, než při generování kandidátů.

range(i,j) vrací čísla menší než j , počínaje i, tedy range(5,10) vrací 5,6,7,8,9 a smyčka for i in range(n+1,10) je tedy projde (tady bylo n=4, n+1=5)

sx je nová dvojice (n,i) [ d for d in days if sx in d] vrací všechna d taková, že d je v days (čili už nalezený den) a sx je v tom d (čili už je ta dvojice použitá). Jestliže se takový den najde, tak to není vhodný kandidát a continue pokračuje dalším cyklem smyčky (tady for i in ...)

return končí funkci a vrací hodnotu (a chybí mi tam return False na konci té funkce, ale buď to tam nedošlo, nebo se prázdná návratová hodnota bere jako False, takže mi to nevynadalo)

Hlavní program začíná po skončení definice funkce cyklem for a in range

Celé je to psané dost humpolácky a jednoduše, protože 10 je malé číslo, rekurze do úrovně 5 a dvě, nebo tři vnořené smyčky prostě znamenají nějaké stovky nebo tisíce průchodů a pro jednorázové použití to dnešní počítače s téměř neomezenou pamětí a rychlostí (pro tyto účely) zvládnou rychle (u mě za 0.011 sec)

A celé je to jen rozepsání toho zadání, když člověk je zvyklý programovat, používat rekurzi a zná trochu prostředky svého jazyka

10 osob ti dá (10^2-10)/2=45 dvojic. To je fakt z zadaných údajů (10 osob) a omezení nesmět se střídat..
A hle ono ti to krásně na 9dní vyjde, že každý den bude pět dvojic (45/9). TO sedí skoro jak šťastný konec pohádky nebo školní úlohy

Připadalo mě to jako otázka ideální pro LLM a protože matematiku neovládám tak jsem se zeptal ještě na doplňující otázky. Snad to pomůže:

Zde je jeden z možných způsobů, jak vytvořit rozvrh pro vaši situaci:

Prvně si pojďme zjistit, kolik celkově různých kombinací dvojic můžeme získat z 10 osob. K tomu můžeme použít vzorec pro kombinace bez opakování:

C(10, 2) = 10! / (2! * (10 - 2)!) = 45 kombinací dvojic

Máme celkem 45 různých dvojic. Nyní chceme tyto dvojice rozdělit do 9 dní tak, aby se neopakovaly. Pro každý den budeme vybírat 5 dvojic.

Dvojice budeme označovat jako A1, A2, B1, B2, atd.

Zde je jeden z možných rozvrhů:

Den 1:

A1, A2, B1, B2, C1

Den 2:

A3, B3, C2, D1, D2

Den 3:

A4, C3, D3, E1, E2

Den 4:

A5, D4, E3, F1, F2

Den 5:

A6, E4, F3, G1, G2

Den 6:

A7, F4, G3, H1, H2

Den 7:

A8, G4, H3, I1, I2

Den 8:

A9, H4, I3, J1, J2

Den 9:

A10, I4, J3, B3, B4

Tento rozvrh zajišťuje, že každý den jsou vybrány 5 unikátních dvojic a žádná dvojice se neopakuje v průběhu 9 dní. Je třeba si dát pozor na to, že se některé dvojice mohou opakovat přes více dní (např. B3 je ve dnech 2 a 9), což je třeba brát v úvahu, pokud by to mělo nějaký vliv na vaši situaci.

Co znamená C() a vykřičník za číslem?

Symbol "C()" se v kombinatorice používá k označení binomického koeficientu. Binomický koeficient C(n, k) udává počet způsobů, jakými lze vybrat k prvků ze skupiny n prvků, a to bez ohledu na pořadí. Vyjádřeno matematicky:

C(n, k) = n! / (k! * (n - k)!)

Kde "n!" znamená faktoriál čísla n, což je součin všech celých čísel od 1 do n.

Vykřičník za číslem je běžně používaný způsob značení faktoriálu. Například "n!" znamená faktoriál čísla n.

V mé předchozí odpovědi jsem použil binomický koeficient pro výpočet počtu různých dvojic z daného počtu osob, což bylo zavádějící. Omlouvám se za to. Pro správný postup vytvoření rozvrhu potřebujete spíše permutace než kombinace.

Pokud chcete, mohu se pokusit znovu vytvořit správný rozvrh na základě permutací a podmínek, které jste uvedl.