Dobrý den,
měl bych dotaz elkově ohledně matematické logiky a pak zvláště ohledně implikace, nejsem si jistý, jestli to chápu správně.
Asi začnu tou implikací, např:
Nechápu proč pokud mám A => B a A je nepravdivé, tak pak už nezáleží na pravdivosti B a implikace je pravdivá. Poté nevím, jak se to bere v rámci tich matematických zápisů, např:
Pro všechna n přirozená čísla, platí že pokud je n dělitelné 4, pak je dělitelné i 2.
(pro všechna n náležící N)(4|n => 2|n)
Je mi jasné, že toto platí, 4|n je postačující podmínka pro 2|n (pokud je číslo dělitelné 4 je automaticky dělitelné i 2) a 2|n je nutná podmínka pro 4|n (pro to aby bylo číslo dělitelné 4 musí být nutně dělitelné i 2)
takže:
A B A => B
0 0 1
0 1 1
1 0 0
1 1 1
pro 4. řádek platí, že pokud je číslo dělitelné 4, pak je dělitelné i 2
3. řádek je blbost
pro 2. řádek pokud číslo není dělitelné 4, pak je dělitelné 2 a je to pravda (úplně nevím, jak to napsat a ani to nechápu, to znamená, že je to pro např. 6 také splněno?)
pro 1. řádek pokud číslo není dělitelné 4, pak není ani dělitelné 2 a je to pravda (taky úplně nevím, jak to napsat a opět to nechápu: např.: číslo 5 není dělitelné 4 ani 2, ale implikace je i tak pravdivá?)
Aktuálně chápu implikaci teda tak, že pokud není první tvrzení správně, tak to druhé ani neřeším, což je asi blbě. (beru jako podmínku)
----------------------
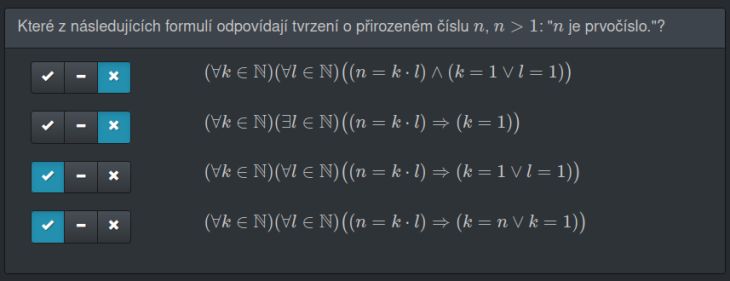
Byl bych rád, kdyby mi někdo, prosím, vysvětlil příklad na obrázku (odpověďi jsou správné, ale k ním jsem došel až po přečtení odpovědí ostatních a stejně úplně nechápu, co se tím myslí).
Vím, že prvočíslo je číslo dělitelné jedničkou a samo sebou.
Takže já bych to napsal asi takhle: (pro všechna n náležící N) (existuje takové k náležící do N) (k|n => (k=1 nebo k = n)) , kde N myslím množinu přirozených čísel, "pro všechna" a "existuje" jsou kvantifikátory, k|n = k dělí n.
A teď podle obrázku (také nechápu proč u každého z těchto zápisů není něco jako: "existuje takové n náležící N"):
1) Pro všechna k náležící N a všechna l náležící N platí, že pokud je n = k*l a (k=1 nebo l = 1), tak je číslo n prvočíslem.
- nevím proč toto tvrzení neplatí, když je skoro stejné jako 3. tvrzení, chápu to tak, že pokud platí n=k*l a (k=1 nebo l = 1) , platí to pro nějaká čísla k a l, přičemž jedno z nich je rovno jedné a to duhé musí tedy být rovno n (což je tedy prvočíslo)
2) Pro všechna k náležící N, existuje takové l náležící N, že pokud je n = k*l, pak je k=1, poté je číslo n prvočíslem.
- jestli to chápu správně, tak např: pro n = 15 je to: 15=1*15 (k=1, l=15), což je očividně blbost (resp. nesplňuje to zadání).
3) Pro všechna k náležící N a všechna l náležící N platí, že pokud je n = k*l, pak je (k = 1 nebo l = 1), n je prvočíslo.
- tady jsem si myslel, že když 1. tvrzení není pravdivé, tak nebude ani toto, protože v nich opravdu nějaký rozdíl nevidím.
4) Pro všechna k náležící N a všechna l náležící N platí, že pokud je n=k*l, pak je (k=n nebo k=1), n je prvočíslo.
- toto jsem předpokládal, že je pravda, ale když si tam dostadím za n=15, pak k=1 a l=15, což platí a také platí, že k = 1, takže by implikace byla taky pravdivá
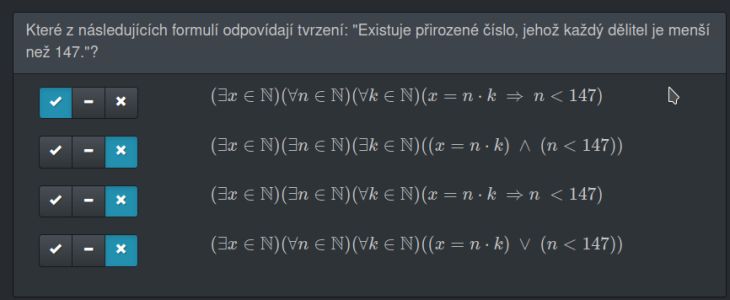
Podobně i druhý obrázek, píše se každý dělitel, tj. k a n jsou dělitelé čísla x proč neověřujeme v tý implikaci i k < 147, tj. ... (x=n*k => (n < 147 a k < 147)), např. číslo x=12345 má dělitele n=1 a k = 12345, což ale nespňuje, že je oba jsou menší než 147, když ověřujeme jen n.
Co je tedy vlastně výstupem těchto mat. zápisu, nějaká množina? pro kterou platí, že splňují dané výroky?
Děkuji Vám za odpovědi.
doplněno 25.08.23 18:19:
Jen jsem začal číst, tak:
*celkově
*těch
...
Omlouvám se za všechny další chyby 
2x
Implikace A => B říká, že z platnosti A plyne platnost B.
Například, že z toho, že A( n je dělitelné 4) plyne platnost B(n je dělitelné 2).
Takže výrok V, tvrdící, že A => B je platný právě tehdy když neexistuje žádný případ, kdy by platilo A a B neplatilo.
Jestliže pro všechna n platí, že pokud je n dělitelné 4, tak je dělitelné i 2, tak je ten výrok V (a tedy ta implikace) pravdivý.
(My všichni víme, že tomu tak je a že "je to očividné")
---
n=4 je dělitelné 4 a tedy i 2. n=8 je dělitelné 4 a tedy i 2. n=12 ... atd. žádný problém.
n=5 není dělitelné 4 a není dělitelné ani 2. n=6 není dělitelné 4 a je dělitelné 2. A ani s tím nemáme problém, protože když to není dělitelné 4, tak nás už nezajímá, čím vším to dělitelné je, protože to nepřinese nic nového k debatě o tom, jestli A => B (jestli z dělitelnosti 4 plyne dělitelnost 2).
Takže pokud A neplatí, tak nás už nezajímá, zda B platí, nebo nikoli, protože to tu implikaci nemůže vyvrátit, ani potvrdit.
---
"Jestli já jsem čínský papež, tak je Měsíc ze syrečků"
"No jo, ale ty čínský papež nejsi"
"Takže mám pravdu, ať už je Měsíc z čeho chce"
Děkuji za odpověď, i když je to pěkně napsané, tak mi to stále ještě není úplně jasné. 
"n=5 není dělitelné 4 a není dělitelné ani 2. n=6 není dělitelné 4 a je dělitelné 2. A ani s tím nemáme problém, protože když to není dělitelné 4, tak nás už nezajímá, čím vším to dělitelné je, protože to nepřinese nic nového k debatě o tom, jestli A => B (jestli z dělitelnosti 4 plyne dělitelnost 2)." Takže když neplatí, že je číslo dělitelné 4, tak už dělitelnost 2 ani netestuji? Tak to ale nechápu, proč je implikace(A=>B) pravdivá když je A nepravdivé. Jestli není číslo dělitelné 4 a je to dělitelné 2 (např: právě ta 6), tak je implikace pravdivá (resp. je tedy celý výrok pravdivý), to znamená, že 6 náleží do nějakého výstupu (asi množiny) toho výroku?
"Implikace A => B říká, že z platnosti A plyne platnost B." Nejvíc mi to opravdu připomíná podmínku, ale tak to podle těch pravdivostních hodnot být nemůže. "z platnosti A" mi nepřipouští případ, kdy A je nepravdivé/neplatné
"Jestli já jsem čínský papež, tak je Měsíc ze syrečků" Úplně nevím, jak můžu mít pravdu, když vím, že první výrok není pravdivý.
Ještě jednou děkuji za odpověď.
Omlouvám se, že se ptám dokola, ale opravdu mi ta implikace přijde nelogická, když je nepravdivý první výrok.
Nevím, čemu přesně v tomto kontextu říkáš "podmínka", ale je docela dobře možné, že máš pravdu
Zkusím ještě jiný případ, kdy pronesu nějaký výrok a nějak se zachovám. Pokud ten výrok poruším, tak jsem Lhář, pokud ho neporuším, tak jsem Poctivec.
Pronesu slib - výrok "Pokud (mě pozveš v Praze na pivo) tak potom (ti vysvětlím implikaci)" A=>B
Jaké jsou možnosti -
- ty mě pozveš, já ti nic nevysvětlím - to je jasné, jsem Lhář, ty jsi svou část splnil, já svou nikoli, svůj slib jsem porušil, , ta implikace neplatí
- ty mě pozveš, já ti to vysvětlím - jsem jasně Poctivec - ty jsi svou část splnil, a já následně svou část splnil taky, svůj slib jsem neporušil, ta implikace platila
- ty mě nikam nepozveš, ale já ti to stejně vysvětlím - jsem Poctivec - ty jsi svou část sice nesplnil, ale já ti to stejně vysvětlil, určitě jsem svůj slib neporušil (implikace platí - nelze dokázat, že by neplatila)
- ty mě nepozveš a já ti nic nevysvětlím - pořád jsem Poctivec - já svůj slib neporušil (implikace platí).
ta implikace je "Pokud A, tak potom B" - porušit se dá jedině tak, že by nastalo A, ale B nenastalo.
Pokud A nenastane, tak se nevyžaduje, aby B nastalo, ale ani se nevyžaduje, aby B nenastalo.
Implikace říká - za podmínky A musí nastat B. Ale implikace neřeší, co se má stát, pokud A prostě nenastane (neplatí, není splněno ...). Implikace není symetrická.
V případě, že A nenastane, tak není možno implikaci porušit, protože implikace mluví pouze o to, co se stane, pokud nastane A.
---
Tím se "implikace" liší od "ekvivalence", která říká A nastane právě tehdy když nastane B (A <==> B), kde pokud A není splněno, nesmí být splněno ani B. Ekvivalence symetrická je.
2x
Obrázek:
Zadání "Které znásledujících formulí odpovídají tvrzení o přirozeném číslu n, n>1, n je prvočíslo"
a pak jsou jednotlivá tvrzení 1)..4) (nečíslovaná, ale snadno očísluješ sám).
Zadání se jinými slovy ptá "která z tvrzení jsou pravdivá?" za předpokladu, že máme nějaké n z N, o kterém víme jen, že je >1 a prvočíslo.
Aby to šlo rozhodnout, tak je to pořeba chápat, které tvrzení je pravdivé pro všechna prvočísla z N, větší než jedna. 4ili tuto podmínku je potřeba připojit před každé z těch tvrzení.
1) pro každé k a každé l platí, že n=k*l a přitom (dál nemusím číst, protože například pro n=3, k=8 a l=12 to zjevně neplatí, nemůže platit tedy ani logický součin a tedy ani celý várok.
2) pro každé k existuje l, že platí "z (n=k*l) plyne, že k=1" - pro n=3, k=8 takové l neexistuje, první část výroku (implikace) neplatí a tedy celý várok platí ("Jestli já jsem čínský papež, ..."),
- ale n=3, k=3, l=1 například spl%nuje první část implikace, ale k=3, takže druhá část není splněná, implikace neplatí a tedy neplatá ani celý výrok 2), protože jsme našli protipříklad
3) pro každé číslo k a každé číslo l platí, že pokud je jejich součin prvočíslo, tak aspoň jedno z nich je rovno jedné. (Ano, to je jinak formulovaná definice prvočísel, to zjevně platí). Tady si povšimneme, že pro naprostou většinu dvojic ta první část implikace neplatí a tudíž se nemusíme ani zaobírat tou druhou částí.
4) pro každé číslo k a každé číslo l platí, že pokud je jejich součin prvočíslo, tak je k rovno jedné, nebo tomu prvočíslu. (opět očividné z definice prvočísel a násobení) (Zase nám vypadají skoro všechny dvojice k,l , ale protože je to implikace, tak nám to nevadí)
---
Druhý obrázek
"Odpovídají tvrzení" = "jsou pravdivá právě tehdy, když je pravdivé to tvrzení" (tehdy a jen tehdy, když) (jsou pravdivá, když je pravdivé a nepravdivá, když je nepravdivé) ...
1) jestliže existuje takové přirozené x, že pro každé n a každé k (která mu jsou v součinu rovna) musí nutně platit, že n<147, tak musí platit i to, že k <147, protože jinak (důkaz sporem) by se mezi dvojicemi musel vyskytnout i dvojice (k,n), pro kterou by to neplatilo.
2) "existuje číslo takové, že jeden z jeho dělitelů je menší než 147" není ekvivalent, protože zahrnujke i čísla, kde druhý dělitel je větší než 147
3) zde stačí volit n=1, pak nám vyjde, že k=x a zahrne nám to i čísla, kde je nějaký dělitel (k) větší než 147 - takže neprázdnost této množiny ještě neznamená nutnou neprázdost množiny ze zadání (řešení tohoto výroku obsahují i x, které nevyhovují omezením ze zadání).
4) Zjevně neexistuje číslo, které by bylo rovno součinu jakýchkoli dvou čísel (z nichž je jedno větší než (nebo rovno) 147) naráz. Ale to se zadáním také nesouvisí.
"1) pro každé k a každé l platí, že n=k*l a přitom (dál nemusím číst, protože například pro n=3, k=8 a l=12 to zjevně neplatí, nemůže platit tedy ani logický součin a tedy ani celý výrok." Pro n=3, k=8 a l=12 to neplatí, ale když vezmu n=3,k=1 a l=3, tak pro to už to platí. Chápu to tak, že si vyberu jen taková k a l, která odpovídají tomu: n=k*l a (k=1 nebo l=1), proč tedy při prvním neúspěchu (k=8, l=12) už celý výrok vyloučím. To je kvůli těm kvantifikátorům? pak ale nechápu, proč by 3.volba měla být správná jen kvůli změně log. součinu za implikaci, když přeci vezmu n=3, k=8 a l=12 pro tu 3.volbu, tak dostanu hned n=k*l nepravdu, tudíž je implikace pravdivá, ale n není rovno k*l.
"2) pro každé k existuje l, že platí "z (n=k*l) plyne, že k=1" - pro n=3, k=8 takové l neexistuje, první část výroku (implikace) neplatí a tedy celý výrok platí ("Jestli já jsem čínský papež, ...")" Pokud takové l není, tak proč považuji k=8 jako správnou volbu, když tomu tak není: n není rovno 8 * l, které existovat nemůže, když je l z N
"Tady si povšimneme, že pro naprostou většinu dvojic ta první část implikace neplatí a tudíž se nemusíme ani zaobírat tou druhou částí." Vyloučili, přeci ta implikace bude pravdivá, tak to uvažujeme jako řešení, ne?
"(Zase nám vypadají skoro všechny dvojice k,l , ale protože je to implikace, tak nám to nevadí)" Asi úplně nevím proč to u implikace nevadí a u toho log. součinu ano.
"musí nutně platit, že n<147, tak musí platit i to, že k <147, protože jinak (důkaz sporem) by se mezi dvojicemi musel vyskytnout i dvojice (k,n), pro kterou by to neplatilo." Např.: pro x=12345, n=1 a k=12345, je pravdivé jak x=n*k, tak i n<147 a k je přitom větší než 147. Pokud bychom uvažovali za x prvočíslo větší než 147, tak nepůjde rozložit jinak než n=1 a k=x nebo k=x a n=1, takže oba dělitelé nebudou větší než 147.
"2) "existuje číslo takové, že jeden z jeho dělitelů je menší než 147" není ekvivalent, protože zahrnujke i čísla, kde druhý dělitel je větší než 147" Kdybychom tam přideli ještě "a k < 147", tak to bude pravdivé tvrzení?
Děkuji za odpověď
2x
Možná ještě jiný přístup.
Implikace (A=>B) říká, že A je postačující (ale nikoli nutnou) podmínkou pro následek B.
----
Pokud je splněno A, pak musí nastat (být splněno) i B. (Je-li n dělitelné 4, nutně musí být sudé - dělitelné 2)
Ale pokud A splněno není, tak B stále nastat může. (Například n=6 není dělitelné 4, ale je sudé - dělitelné dvěma.) Toto implikaci A=>B nevyvrací.
Ale pokud A splněno není, tak B také nastat nemusí . (Například pro n=3 není dělitelné 4, a sudé taky není) Ani toto implikaci A=>B nevyvrací.
Implikaci A=>B by vyvrátilo jedině to, kdyby nastala příčina A a nenastal následek B.
.
Čili pokud není splněna podmínka v implikaci, tak není zaručen ani výsledek, ale o tom implikace vůbec nemluví a tudíž ji to nemůže vyvrátit.
.
To, že implikace tvrdí, že z pravdy plyne pravda a z nepravdy cokoli, není chyba její definice, ale naopak naprosto klíčová (a definiční) vlastnost.
Pokud je implikace platná a první tvrzení není platné, tak druhé tvrzení ani řešit nemusíš, může být libovolné.
Pokud je implikace platná a první tvrzení je platné, tak druhé tvrzení nutně musí být platné.
doplněno 26.08.23 06:06:
A ještě jeden pohled.
Pokud máš dva výroky A a B (kde každý může být buď pravda, anebo nepravda, nic jiného) a nějakou operaci O která z nich dělá jeden výrok, který bude buď pravda, anebo nepravda, nic jiného, tak když si uděláš tabulku pro A a B, tak bude mít celkem 4 řádky a pro každý řádek přesně jeden výsledek.
Ty 4 výsledky pak určují tu operaci O.
Těch možných čtveřic a tedy operací je celkem 2^4=16.
Většina z nich dostala nějaké jméno, podle toho co lidem připomínala.
Například logický součin má ve výsledku jedničku jen tam, kde jsou samé jedničky (jako při násobení) a znamená to, že výsledek je pravda, jen jsouli pravda všechny výroky.
Logický součet má nulu jen tam, kde jsou samé nuly (jako při sčítání) a znamená to, že výsledek je pravda pokud je pravda aspoň jeden výrok.
Ekvivalence má jedničku jen tam, kde jsou oba výroky jedničky, nebo oba nuly a znamenáto, že platí, pokud jsou výroky stejné.
A implikace má nulu jen tam, kde je na začátku jednička a druhá je nula a znamená to, že platí, pokud z (pravdivosti) prvního výroku vyplývá (pravdivost) druhého.
Definicí je to rozložení nul a jedniček, ten popis je jen popis, aby lidi intuitivně věděli, jak s tím pracovat.
Ale ono jak jinak bys chtěl vyjádřít, že B vyplývá z A (nikoli naopak), než právě tím, že pokud je A 1, tak B musí být 1, zatímco pokud je A 0, tak na hodnotě B nesejde?
doplněno 26.08.23 06:13:
A podobná zkratka je i u toho součtu - pokud je první výrok pravda, na na hodnotě druhého nesejde a celý výrok je pravda. (například "2 je sudá NEBO Měsíc je ze syrečků" je zaručeně pravda)
A u logického součinu, pokud je první výrok nepravdivý, tak na hodnotě druhého nesejde a celý výrok je nepravda (například "1 je sudá A PŘITOM Měsíc obíhá Zemi" je zaručeně lež - obojí bez ohledu na nějaký Měsíc)
Děkuji hezky popsané.
Ještě taková drobná otázečka k těm kvantifikátorům.
Když budu uvažovat první obrázek a v něm 1. a 3. tvrzení.
Tak pokud je tam obecný kvantifikátor, tak to musí platit pro všechny (k,l) prvky z N, takže např: pokud n=6
pak budou možnosti jako:
k=1, l=6, tak je první tvrzení (s disjunkcí) pravdivé, 3. tvrzení s implikací je také pravdivé
k=1,l=7, tak je první tvrzení (s disjunkcí) nepravdivé, 3. tvrzení s implikací je pravdivé
k=2,l=3, tak je první tvrzení (s disjunkcí) nepravdivé, 3. tvrzení s implikací je také nepravdivé
k=5,l=12, tak je první tvrzení (s disjunkcí) nepravdivé, 3. tvrzení s implikací je pravdivé
...
A druhý příklad: pro n = 5
k=1,l=5, tak je první tvrzení (s disjunkcí) pravdivé, 3. tvrzení s implikací je pravdivé
k=1,l=6, tak je první tvrzení (s disjunkcí) nepravdivé, 3. tvrzení s implikací je pravdivé
k=2,l=3, tak je první tvrzení (s disjunkcí) nepravdivé, 3. tvrzení s implikací je pravdivé
k=2,l=8, tak je první tvrzení (s disjunkcí) nepravdivé, 3. tvrzení s implikací je pravdivé
...
Takže pokud to chápu správně, tak když se bude procházet přes všechna n a pro každé z nich přes všechna možná k a l, tak pokud bude dané tvrzení pravdivé pro dané n a všechny možné případy k a l, tak je poté pravdivé celý výrok?
Např. první příklad ukazuje za n=6, ale jakoby průchodem přes všechna k a l jsme dospěli i k "k=2 a l=3", pro které je implikace nepravdivá, tj. je napravdivý celé tvrzení pro zadané n (n=6).
Ale druhý případ ukazuje, že když za n zvolíme opravdu prvočíslo (např. n=5), tak pak bude implikace pravdivá pro všechny možné varianty k a l, tj. zjistili jsme, že n (teď tedy 5) je opravdu prvočíslo.
Mimochodem, proč není u toho prvního obrazku nějak definované x (např.: existuje nebo pro všechna x z N)?
Děkuji za pomoc.
U toho prvního obrázku je to zadaní jinými slovy takto: ("pro přirozené n" je to samé jako "pro n elementem N", nebo jak píšu zkráceně "pro n z N" - čili je to zadané. Stejně tak pokud se otázka ptá na zálečitosti okolo n, aniž by řekla, že pro zadané n, nebo že existuje n, nebo to nějak jinak upřesnila, tak se rozumí, že to musí platit pro libovolné n, (které splňuje případné další požadavky))
Pro každou z následujících formulí řešte úlohu:
Pro každé n z N platí, že (=>
pokud je n>1 tak potom (=> je výrok "n je prvočíslo" ekvivalentní (<==> formuli.
Začneme s první formulí
začneme s n=1 (je přirozené, tak to zatím platí) pokud je n>1 (to neplatí) tak potom (=> z nepravdy plyne cokoli, čili pro toto n z N to platí
pokračujeme s n=2 (je přirozené, tak to zatím platí) pokud je n>1 (taky platí) tak potom (=> (z pravdy musí plynout pravda, musíme tedy dořešit, zda plyne) "n je prvočíslo" (pravda) je ekvivalentní (? zjišťujeme?) výroku "pro všechny k, pro všechny l platí (n=k*l) ^ (k=1 v l=1)"
Tady už se nám to zadrhne protože hned pro první k=1 l=1 neplatí (2=1*1) a tudíž neplatí ani celý součin a tudíž neplatí, že "pro všechny K, pro všechny l..."
tudíž má ekvivalence vlevo pravdu a vpravo nepravdu a neplatí, tudíz první formule není ekvivalentní s "n je prvočíslo" a dostává X
-----
pro třetí formuli:
začneme s n=1 (je přirozené, tak to zatím platí) pokud je n>1 (to neplatí) tak potom (=> z nepravdy plyne cokoli, čili pro toto n z N to platí (jako minule, ještě že máme ty implikace : ) )
pokračujeme s n=2 (je přirozené, tak to zatím platí) pokud je n>1 (taky platí) tak potom (=> (z pravdy musí plynout pravda, musíme tedy dořešit, zda plyne) "n je prvočíslo" (pravda) je ekvivalentní (? zjišťujeme?) výroku "pro všechny k, pro všechny l platí (n=k*l) => (k=1 v l=1)"
Tady už se nám to NEzadrhne protože hned pro první k=1 l=1 neplatí (2=1*1) a tudíž z nepravdy plyne cokoli, nemusíme to řešit, je to v pořádku, jdeme dál
Tady už se nám to NEzadrhne protože hned ani pro k=1 l=2 - platí (2=1*1) a tudíž z pravdy musí plynout pravda, ale k=1, logický součet má pravdivý výrok, druhý výrok nemusíme řešit, celá závorka je pravda, z pravdy nám tedy plyne pravda, je to v pořádku, jdeme dál
a pro každou další kombinaci nám buď vyjde že neplatí n=k*l a díky implikaci nemusíme řešit zbytek a je to pravda
(tady je vidět, jak nám pomáhá s filtrováním, že u implikace z nepravdy plyne cokoli, takže pokud to nesplní tu rovnici n=k*l tak můžeme přejít k dalšímu kroku)
nebo nám vyjde, že jsme zrovna vytáhle taková k,l, že n=k*l a teda musíme řešit zbytek, ale protože n=2 je prvočíslo, tak je určitě k nebo l rovno jedné a tudíž to platí.
takhle projdeme všechna k,l a víme, že pro n=2 to platí.
podobně pro n=3 to bude vycházet naprosto obdobně
pro n=4 se to zadrhne u k=2,l=2, kde nám vyjde, že to neplatí, ale zárověň nám i u levé strany ekvivalence vyšlo, že 4 není prvočíslo a tedy nepravda <==> nepravda a je pořád dobře
pro n=5 to zase projde jako u předchozích prvočísel ...
pro n=6 to zase neprojde kvůli 2,3 ale 6 není prvočíslo, takže ekvivalence nepravda,nepravda vyjde a pokračujeme dál až do vyčerpání přirozených čísel (nebo si v době konečné dokážeme pár vět o indukci a odvodíme si, že to platí pro všechna čísla)
---
Takže nám nakonec vyjde, že 3) je ekvivalentní "n je prvočíslo" a dáme jí fajfku (souhlasné zaškrtávátko)
Takže pokud to chápu správně, tak když se bude procházet přes všechna n a pro každé z nich přes všechna možná k a l, tak pokud bude dané tvrzení pravdivé pro dané n a všechny možné případy k a l, tak je poté pravdivé celý výrok?
Ano, chápeš to správně.
Mimochodem, proč není u toho prvního obrazku nějak definované n (např.: existuje nebo pro všechna n z N)?
Ono to tam definovaná je, jen ne tak okatě: "... odpovídají tvrzení o přirozeném číslu n, n>1 ..."
tady je definované, že n je elementem N (akorát že slovně).
"Ono to tam definovaná je, jen ne tak okatě: "... odpovídají tvrzení o přirozeném číslu n, n>1 ..." tady je definované, že n je elementem N (akorát že slovně)." Aha, tak to jo, já myslel, že se to bude muset ještě napsat do toho tvrzení tou matematickou logikou.
Každopádně děkuji za pomoc, už je mi to jasnější
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.