Goniometrie a tabulky

Očekává se, že znáš některé základní hodnoty goni, fci, nebo že alespoň umíš pracovat s touto tabulkou:

Nakreslite si graf funkcie sinus a kosinus, na x os date stupne od 0 po 360, na y os hodnoty funkcie. Potom staci vediet, ze sinus 45 stupnov = 0.707 cos 45 = 0.707

a v grafu odcitat, ako sa hodnoty opakuju alebo menia znamienko

mozete aj vyuzit suctove vzroce sin (x + y) a cos (x + y) a vyuziy, ze sin 0 = 0 cos 90 = 1

135 = 90 + 45

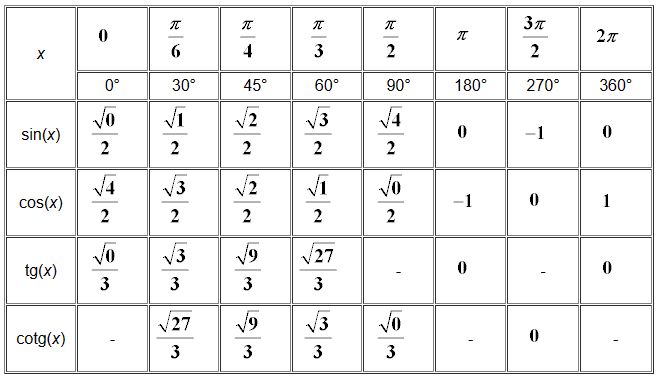
Tabulky obsahují hodnoty jen pro jeden kvadrant, protože funkce je periodická a navíc se hodnoty z prvního kvadrantu opakují v dalších. To se hodí při programování, kdy nemusíte do programu ukládat celých 360° ale jen 90° (mnozí ohrnou nos, že dneska je paměť levná a neni potřeba tak šetřit, ale to je lepší dát tam podrobnější tabulku do 90°než 4x totéž).

A na základě té periodicity a sudosti a lichosti funkce a tak jsou na to postupy, jak určit hodnotu v dalších kvadrantech. Když zůstaneme u intervalu 0-360, tak:

0-90 je v tabulkách

90-180 hledá se úhel chybějící do 180

180-270 hledá se úhel přesahující 180

270-360 hledá se úhel chybějící do 360

Pak jepotřeba určit znaménko a na to je nejlepší si představit graf té funkce, pak zjistíte, že pro kvadranty I, II, III a IV jsou postupně tato znaménka

sin: +,+,-,-

cos +,-,-,+

Vsadím se, že tohle jste si někdy na hodině říkali a určitě to bude i v učebnici. Nebo už i matematika se dostala do systému jakým se učí jazyky, jakože se nejdřív napíše test, pak se dělají cvičení a teprve poté se látka vysvětlí (přesně tímto způsobem byla koncipovaná učebnice anngličtiny, kterou jsme používali, naštěstí po dvou lekcích pani učitelka uznala, že to opravdu neni dobrý postup).

Zdravím.

V jednotkové kružnici je vidět, že sin 135°=sin 45° a že cos 315°=cos 45°. V té jednotkové kružnici lze "najít" rovnoramenný pravoúhlý trojúhelník (jeho vnitřní ostré úhly jsou každý 45°) s přeponou délky 1 (poloměr té jednotkové kružnice). V něm lze vypočítat (Pythagorovou větou: 1²=x²+x²) délku odvěsny x. Vyjde jedna lomeno druhá odmocnina ze dvou, po usměrnění tohoto zlomku vyjde druhá odmocnina ze dvou lomeno dvěma, což je přibližně 0,707. A ze vzorce pro sinus (protilehlá odvěsna ku přeponě) a pro kosinus (přilehlá odvěsna ku přeponě) lze zjistit, že obě hledané hodnoty jsou 0,707...