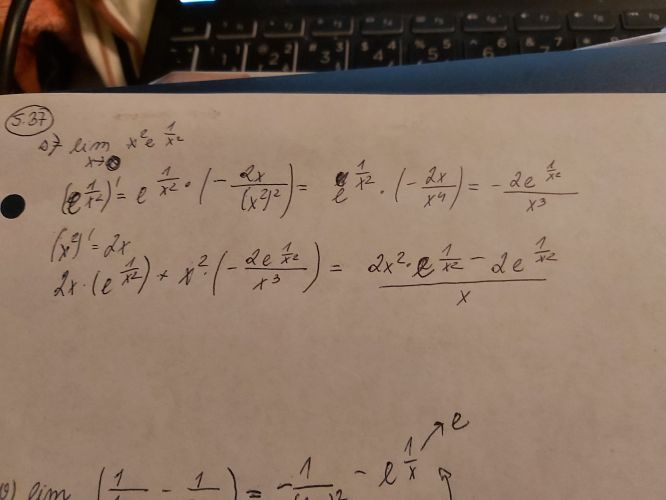Jak vypočítat priklad pomoci LHospitala?

Zdravím,

LHospitalovo pravidlo je používáno v případě limity podílu dvou funkcí.

Ve Vašem zadání je zadán součin dvou funkcí a sice funkce x ² a funkce e ^1/x2

Je to typ limity nula krát nekonečno

Tady je odkaz na video M. Valáška

Tady je odkaz na soubor, kde je popis výpočtu v kapitole 1.3

mathonline.fme.vutbr.cz/...

Po nahrazení x² výrazem 1/x^-2 je limita takto:

= lim _{x →0} 1/x^-2 . e^1/x2 = lim _{x →0} e^1/x2 / x^-2

Po dosazení 0 do tohoto výrazu vzniká typ limity nekonečno/nekonečno

Zvlášť zderivovat horní funkci a zvlášť zderivovat spodní funkci

= lim _{x →0} e^1/x2 . (-2x^-3) / -2 . x^-3

Po vykrácení -2 . x^-3 je

= lim _{x →0} e^1/x2 = nekonečno

Já vidím, že se v závorce x^2 vykrátí a zbyde e, na to nepotřebuju lhopitala. Je to zvláštní, že se vykrátí, není jeden z exponentů jiný, zapsala jste si příklad správně?

lim x->0 (x^2*e*1/x^2)=e*lim x->0 (x^2*1/x^2)=e*lim x->0 (x^2/x^2)=e*lim x->0 (1)=e

Nekonečno, gde jste ho vzala, že má tak vyjít?

Viz níže, jde to i bez L´Hospitalova pravidla