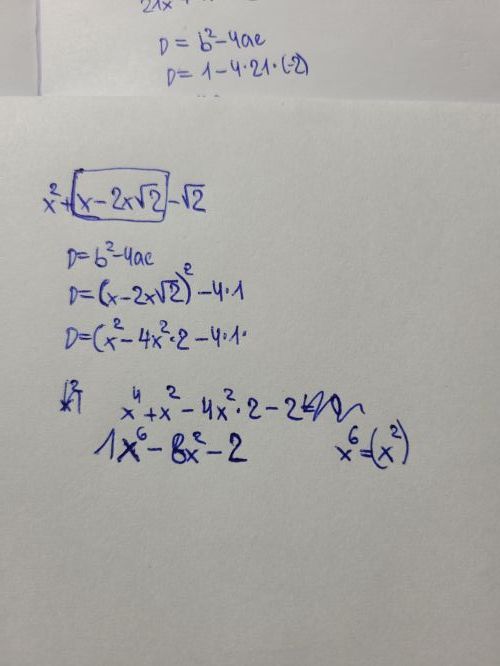Nejste přihlášen/a.
1x
Mimochodem, ten tvůj poslední řádek s diskriminantem, to je velká chyba!
Pokud umocňuješ závorku se součtem či rozdílem, musíš použít vzorec: (a+b)² = a² + 2ab + b², respektive v tomto případě (a-b)² = a² - 2ab + b²
Jinými slovy, (a+b)² SE NEROVNÁ a² + b² !
Pokud nevíš proč, představ si, jak bys počítala (a+b)² bez vzorce. Napsala by sis (a+b)*(a+b), pak bys roznásobovala, vyšlo by ti a² + ab + ab + b², čili a² + 2ab + b² a to je ten vzorec, který tě k tomu dovede rychleji.
0x
Tady je řešení se stručným popisem. Klíčové je použití substituce, důležité je také použití vzorce. Vzorce (a±b)² a a²-b² se určitě naučte, udělejte si na to minimálně 20 příkladů. Na nich se potom dále staví hodně různých věcí, třeba kuželosečky bez jejich znalosti nemáte žádnou šanci zvládnout. Můj výsledek je 100% správný, ověřil jsem to přes počítač. Kdyby něco nebylo jasné, ptejte se.
Nemáte zač ![]()
0x
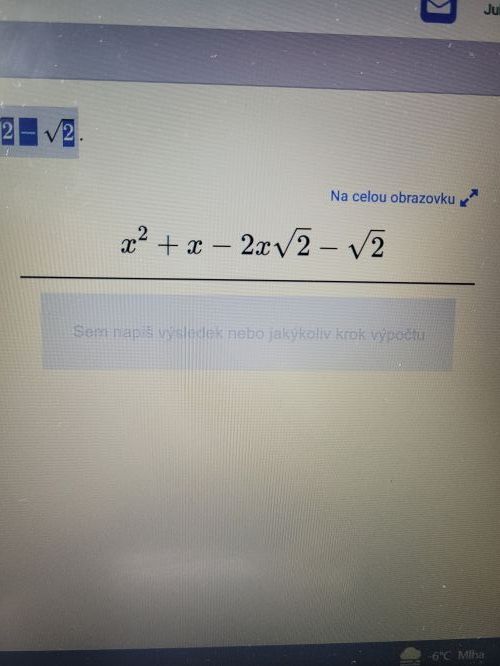
x2 + x - 2x.odm(2) - odm(2)
x2 + x.(1 - 2.odm(2)) - odm(2)
a = 1
b = 1 - 2.odm(2)
c = - odm(2)
D = b2 - 4ac
D = (1 - 2.odm(2))2 - 4.1.(-odm(2))
D = 1 - 4.odm(2) + 4.2 + 4.odm(2)
D = 9
x1,2 = (-b ± odm(D))/2a
x1,2 = (- 1 + 2.odm(2) ± odm(9))/2
x1,2 = (- 1 + 2.odm(2) ± 3)/2
x1 = 1 + odm(2)
x2 = -2 + odm(2)
x2 + x - 2x.odm(2) - odm(2) = ( x - (1 + odm(2)) ) . (x - (-2 + odm(2)) ) = (x - 1 - odm(2) ) . (x +2 - odm(2) )
0x
Převod výrazu na součinový tvar znamená najít kořeny toho polynomu (zde druhého řádu a tedy řešitelné se znalostmi základní školy) a ty potom pro vytvoření součinového tvaru použít
(x-x1)(x-x2)
x je proměnná
x1 a x2 jsou kořeny té kvadratické rovnice (která vznikne tím, že se k výrazu připíše =0)
jinak tu snad vše bylo řečeno včetně výsledku
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.