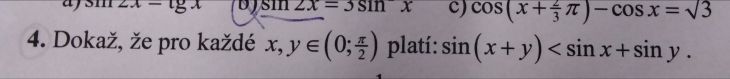Jak vypočítat příklad

Po pravdě taky nevím, asi bych si vykreslil graf, ale to neni důkaz. Zkusil bych ten rozklad, případně jestli existuje i vzorec pro sinx+siny tak i ten, a dále upravit tu nerovnici do tvaru, ze kterého by bylo zřejmé, že je platná pro libovolnou dvojici [x y] z daného intervalu.

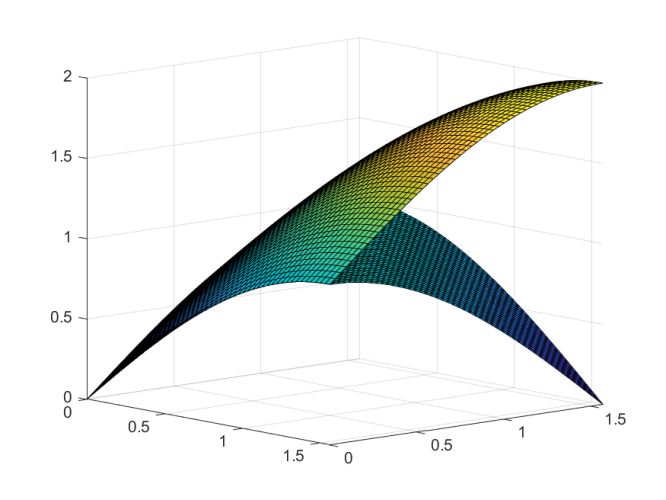
Ten graf je otázka chvilky, tak jej přikládám, do nerovnice se mi nechce. Jak je z grafu vidět, tak od nuly (ne včetně) to opravdu platí, a zdá se že i dál, než do pi/2 a teď to jen dokázat.

Zde je sekvence příkazů Matlabu:

[X,Y] = meshgrid(0 : (pi/100) : (pi/2),0 : (pi/100) : (pi/2));
Z = sin(X) + sin(Y);
Z2 = sin(X + Y);
surf(X,Y,Z)
hold on
surf(X,Y,Z2)
legend(Z,Z2)

Po rozepsání levé strany máme sin(x)*cos(y) + cos(x)*sin(y), přičemž v otevřeném intervalu (0,90) je hodnota kosinu z otevřeného intervalu (0,1).

sin (x + y) = sin x . cos y + cos x . sin y

sin x . cos y + cos x . sin y < sin x + sin y

0 < sin x + sin y - sin x . cos y - cos x . sin y

0 < sin x - sin x . cos y + sin y - cos x . sin y

0 < sin x . (1 - cos y) + sin y . (1- cos x )

sin x je v intervalu (0; π/2) kladná hodnota

(1 - cos y) je v intervalu (0; π/2) kladná hodnota

sin y je v intervalu (0; π/2) kladná hodnota

(1- cos x ) je v intervalu (0; π/2) kladná hodnota

tedy

sin x . (1 - cos y) + sin y . (1- cos x ) je v intervalu (0; π/2) kladná hodnota