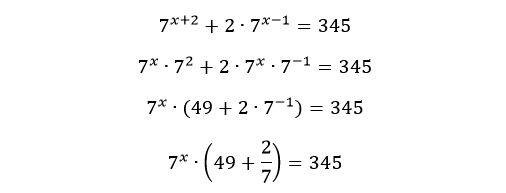Nazdar, mám problém s tímto příkladem, netuším co s ním už od prvního kroku. Většinou v takovém případě použiju PhotoMath abych dostal radu jak začít ale v tomto případě nechápu už první krok - vytknutí 7x-1.
Úprava z aplikace mi absolutně nedává smysl i když se potom dopočítá správného výsledku (1). Předpokládám že je to tím že neumím pořádně vytýkat avšak když něco vytknu tak vynásobením závorky bych se měl dostat zpět k původnímu výrazu ne? To mi přijde nemožné když je v závorce i ta dvojka.
Obrázek 1 - zadání; obrázek 2 - řešení PhotoMath
Otázky: 1) Kde se tam vzala ta trojka? (zelený rámeček)
2) Jaktože je dvojka uvnitř závorky ze které se vytklo 7x-1 (pokud to není jen blbě zapsané aplikací)
3) pokud to teda jen aplikace blbě zapsala, jak by se to tedy mělo zapisovat a počítat správně?
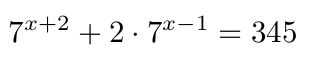

2x
Zdravím.
O tom, že je vytknutí správné, se lze přesvědčit roznásobením výsledného výrazu (při násobení se exponenty sčítají, proto 3+x-1 a oba sčítance v závorce je nutno výrazem 7x-1 vynásobit...): (73 + 2)·7x-1 = 73+x-1 + 2·7x-1 = 7x+2 + 2·7x-1
doplněno 03.11.22 19:09:
Omlouvám se, že ta jednička z exponentu x-1 "utekla" na další řádku...
0x
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.