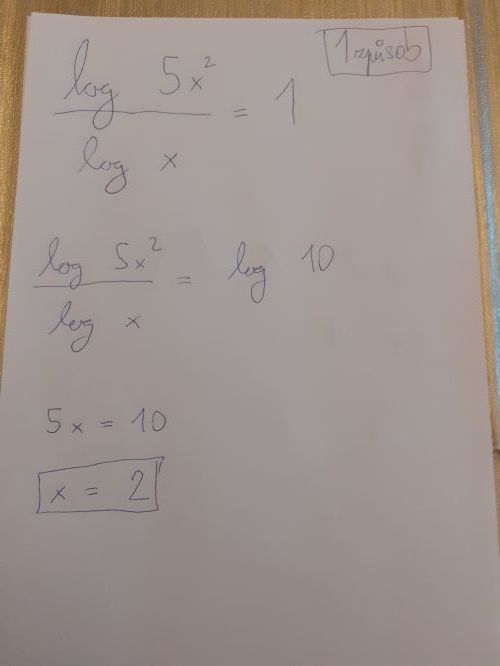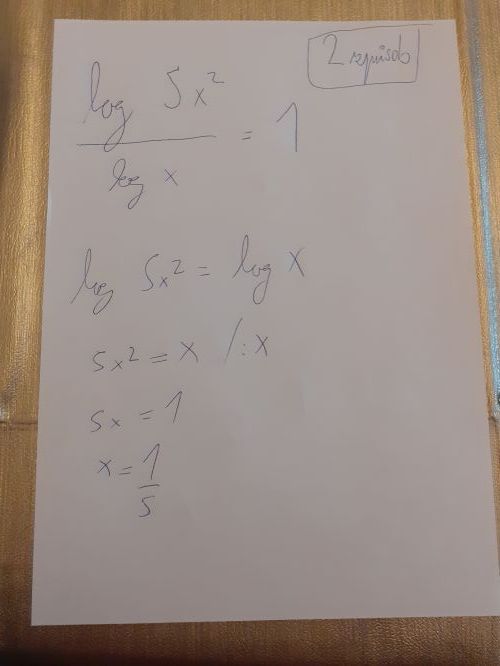Dobrý den,
Nejsem si jist který postup řešení je správný
Máme tuto rovnici: vsechny log jsou o základu 10
(Log 5x^2) / (log x) =1
1.postup
Upravím ze si pravou stranu prevedu na logaritmus o zakladu 10 z cisla 10, abych dostal logaritmy o stejnych zakladech
(log 5x^2)/(log x) = log 10
Dostavam 5x^2/x = 10 => 5x = 10 => x = 2
Druhy postup: vynasobím rovnici jmenovatelem levé strany ( výrazem log x)
(Log 5x^2)/(logx)= 1
Dostanu : log 5x^2= log x
Logaritmy mam o stejnych zakladech, tudi platí 5x^2= x => 5x = 1 => x = 1/5
Vidíme že vyšli dva ruzne kořeny. V prvním postupu vyšlo x = 2. Ve druhem x= 1/5
Nevíte jaky postup je správný?
PS: Pro jistotu zasílám i tištěný postup
Děkuji moc za Váš čas
![Jak resit tuto logaritmickou rovnici]()
![Jak resit tuto logaritmickou rovnici #2]()
Nejsem si jist který postup řešení je správný
Máme tuto rovnici: vsechny log jsou o základu 10
(Log 5x^2) / (log x) =1
1.postup
Upravím ze si pravou stranu prevedu na logaritmus o zakladu 10 z cisla 10, abych dostal logaritmy o stejnych zakladech
(log 5x^2)/(log x) = log 10
Dostavam 5x^2/x = 10 => 5x = 10 => x = 2
Druhy postup: vynasobím rovnici jmenovatelem levé strany ( výrazem log x)
(Log 5x^2)/(logx)= 1
Dostanu : log 5x^2= log x
Logaritmy mam o stejnych zakladech, tudi platí 5x^2= x => 5x = 1 => x = 1/5
Vidíme že vyšli dva ruzne kořeny. V prvním postupu vyšlo x = 2. Ve druhem x= 1/5
Nevíte jaky postup je správný?
PS: Pro jistotu zasílám i tištěný postup
Děkuji moc za Váš čas
2 odpovědi na otázku
Řazeno dle hodnocení
Přihlásit se k odběru odpovědí z této otázky:
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.