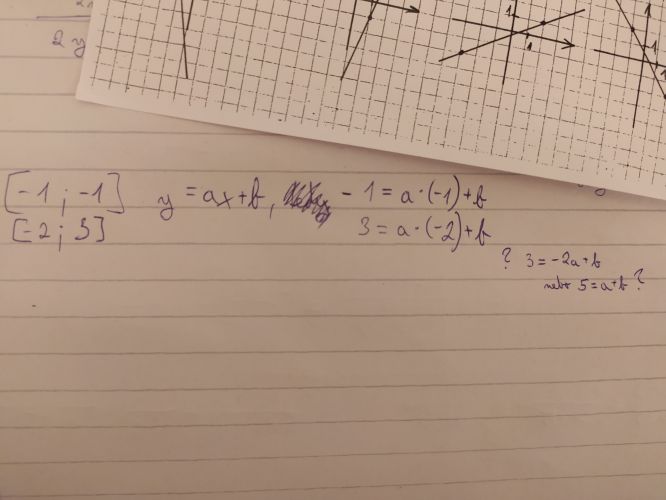Nejste přihlášen/a.
2x
Asi se tážete spíš na rovnici funkce, jejímž grafem je ten daný graf.
Pokud ano, tak lze počítat takto:
1. Grafem je přímka, jedná se tedy o graf lineární funkce. Lineární funkce má rovnici y = ax + b. A k jejímu určení potřebujeme znát 2 body.
2. U prvního grafu jsou vyznačené body grafu [-1,-1] a [-2,3]. Protože oba body leží na grafu funkce (jsou prvky grafu), jejich souřadnice musí vyhovovat rovnici. Musí tedy plati
- pro 1. bod [x,y] = [-1,-1]: y = ax + b, tedy -1 = a. (-1) + b
- pro 2. bod [x,y] = [-2,3]: y = ax + b, tedy 3 = a.(-2) + b
3. Vyřešíme soustavu rovnic a získáme tak koeficienty a, b.
-1 = a. (-1) + b
3 = a.(-2) + b
4. Dosadíme tato čísla a, b do rovnice y = ax + b.
---------------------------------------------------------------------
Jiná možnost je, že se podívám na graf a hned vidím:
- přímka protíná osu y v bodě -5, tedy b = -5
- graf je klesající, tedy a bude záporné a > 0
...
Tuto další možnost bych použila pro kontrolu svého výsledku.
3.
Zdravím.
Ze sestavené soustavy dvou lineárních rovnic o dvou neznámých vypočítat hodnotu a i b a tyto zjištěné hodnoty dosadit za a a b do obecné rovnice lineární funkce (do rovnice y=a*x+b)...
0x
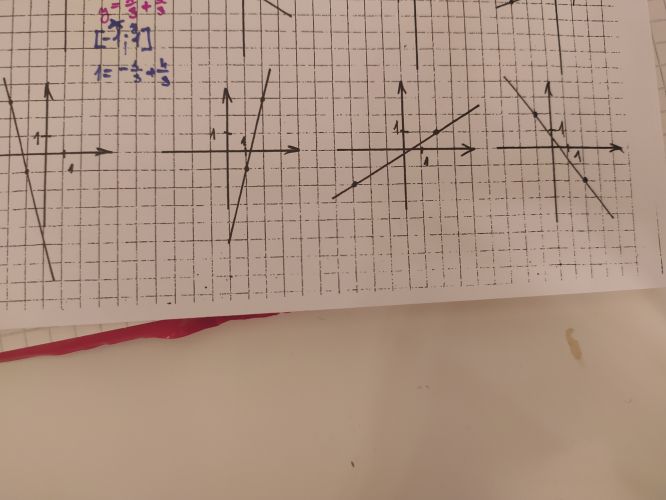
Z leva do prava
první:
y=-4x-5 (to lze přímo vyčíst, když se o jedno zvětší x, o kolik se zvětší y? o -4; mínus pět je vzdálenost bodu[0,0] a průsečíku funkce s osou y tedy [0,5])
druhý:
y=4x-5 (to lze přímo vyčíst, když se o jedno zvětší x, o kolik se zvětší y? o 4; mínus pět je vzdálenost bodu[0,0] a průsečíku funkce s osou y tedy [0,5])
třetí:
Když se x zvětší o 1, o kolik přibude y...o 3/5. Kde se přímka protkme s osou y...Zjistíme z podobnosti trojúhelníka...2-3*3/5=0.2...2 se vzala z vzdálenosti bodu [-3, -2] a přímky x,trojka je vzdálenost bodu [-3, -2] a osy y,... y=3/5x-0,2
čtvrtý:
Když se x zvětší o 1, o kolik přibude y...o -4/3. Kde se přímka protkme s osou y...Zjistíme z podobnosti trojúhelníka...2-1*4/3=2/3...2 se vzala z vzdálenosti bodu [-1, 2] a přímky x,jednička je vzdálenost bodu [-1, 2] a osy y,... y=-3/4x+2/3
-----------
Nezapomeňte:
rostoucí funkce ... u x kladné znamínko...y=+ax+b
klesající funkce ... u x záporné znamínko...y=-ax+b
je-li prusečík osy y a funkce pod [0,0] ... absolutní člen odečítáme...y=ax-b
je-li prusečík osy y a funkce nad [0,0] ... absolutní člen přičítáme ...y=ax+b
----------
Zkontrolovat si to můžete třeba v Geogebře.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.