Ahoj, jsem bezradný, skončil jsem u toho, že to má být větší než nula. Předem děkuju
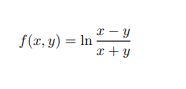
0x
Ano, zlomek má být kladný, tj. platí, že: a) čitatel i jmenovatel je kladný, nebo b) čitatel i jmenovatel je záporný. Úlohu bych řešil graficky v soustavě souřadnic.
Např. nerovnici x > y znázorníme takto: Zakreslíme přímku x = y, vzniknou dvě poloroviny. Vybereme libovolný bod jedné poloroviny a zjistíme, zda pro něj daná nerovnost platí, nebo neplatí, např. bod [2; 0] nerovnici vyhovuje, tj. nerovnici x > y vyhovují všechny body v modré polorovině (kromě hraniční přímky): wolframalpha.com/... (nejsou tam zakreslené osy x, y).
Nakonec by mělo vyjít wolframalpha.com/...
0x
x - y ≠ 0
x ≠ y
x + y ≠ 0
x ≠ - y
(x -y ) / (x + y) > 0
Buď
x - y > 0 a současně x + y > 0
a tedy
x > y a současně x > - y
nebo
x - y < 0 a současně x + y < 0
a tedy
x < y a současně x < - y
Definičním oborem dané funkce dvou proměnných je část "2D"plochy dané osami x,y
doplněno 30.05.21 09:17:
Odkaz na vyřešený příklad sem dal Mirek
Toto je znova ten odkaz:
Ty dvě "šikmé čáry", tedy grafy funkcí
y = x
y = - x
mají být čárkovaně.
Je potřeba tam doplnit osu x a osu y (prochází průsečíkem těch "šikmých čar")
Tady je odkaz na soubor, kde jsou další příklady na definiční obor funkce dvou proměnných. Je na těch obrázcích vidět, jak nakreslit šrafování a jak nakreslit přerušovanou "čáru".
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.