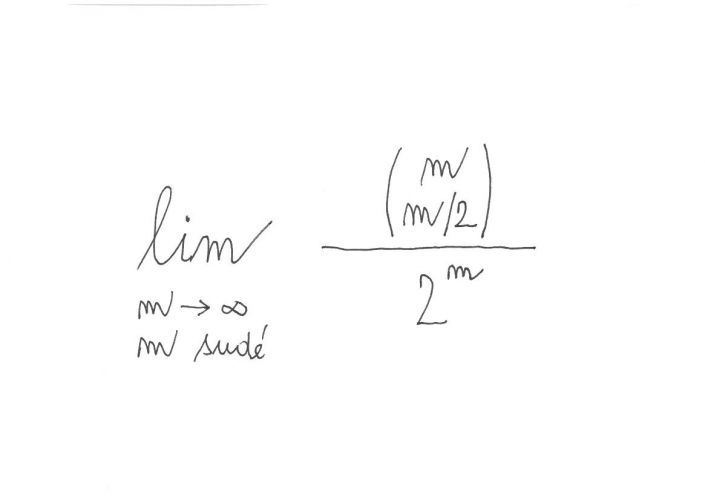limita pro m k nekonečnu, m sudé, podílu: (m nad m/2) / 2m
0x
Čitatel zlomku je kombinace, viz. např. vzorec na str. 3 souboru, na který je tento odkaz:
Čitatel zlomku lze přepsat takto:
m! : [(m/2)! krát (m/2)!]
Je možné, že ta limita je rovna 1.
Když m zvýšíme o 2, tak
velikost jmenovatele zlomku se zvýší čtyřikrát.
velikost čitatele zlomku se zvýší
( (m+2)! : [( (m+2)/2 )! krát ( (m+2)/2 )! ] ) / ( m! : [(m/2)! krát (m/2)! ])
krát
Úpravou tohoto výrazu lze možná dokázat, že limita tohoto výrazu pro m se blíží nekonečnu je 4
" Pokusně":
(12 nad 6) je 924
(14 nad 7) je 3432
3432 : 924 = 3,71
---
(14 nad 7) je 3432
(16 nad 8) je 12870
12870 : 3432 = 3,75
----
(20 nad 10) je 184756
(22 nad 11) je 705432
705432 : 184756 = 3,81
Dobrý den, děkuji za Váš zájem. Váš příspěvek jsem prošel a nenalezl jsem v něm žádnou chybu. Jediný problém (nejde o chybu!) mi činí věta: "Je možné, že ta limita je rovna 1."
Jen zrekapituluji, že když označíme
P(m) = (m nad m/2) / 2m
pak Vy jste dokázal, že lim ( P(m + 2) / P(m) ) = 1 pro x přirozené, sudé a blížící se nekonečnu.
Z této skutečnosti však bohužel žádný závěr o hodnotě limity nelze vyvodit. Doložím to na protipříkladu:
Mějme funkci f(x) = 5 + 1/x
lim ( f(x + 2) / f(x) ) = 1 pro x blížící se nekonečnu,
a přesto lim f(x) = 5 pro x blížící se nekonečnu.
Lze však nahlédnout, že
lim P(m) pro x přirozené, sudé a blížící se nekonečnu
se nemůže rovnat 1. Vyplyne to z následujícího popisu úlohy, od které se toto vše odvíjí:
Hodíme m-krát mincí (m sudé). Jaká je pravděpodobnost P(m), že padne právě m/2-krát orel a m/2-krát panna?
Řešení: P(m) = (m nad m/2) / 2m
Jelikož jde o pravděpodobnost, tak pro každé přirozené sudé m musí P(m) ležet vždy v uzavřeném intervalu od 0 do 1.
P(2) = 0,5
P(4) = 0,375
P(6) = 0,3125
P(m) je klesající posloupnost.
P(1000) = 0,025 (přibližně)
A pokud nás zajímá, zda tato posloupnost nikdy nepřekročí nějaké malé kladné číslo, anebo zda se naopak s rostoucím m blíží k nule bez omezení, tak je řeč právě o oné výchozí limitě.
Vypadá to, že se blíží k nule, ale ...
Jestli stačí výsledek, limita je rovna nule, viz wolframalpha.com/...
Postup mě bohužel nenapadá, třeba by věděl někdo tady forum.matematika.cz/...
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.