Paraboly-průsečíky, souřadnice, rovnice tečen

Za 4.

1, dosadit za průsečíky s x: dosadit do rovnice za y=0, s y: dosadit za x=0

2, Vyjádřit jednu proměnou z jedné dovnice a dosadit do druhé. vyjde pak y=číslo nebo x=číslo, to číslo pak dosadit do jedné z rovnic k dourčení druhé souřadnice

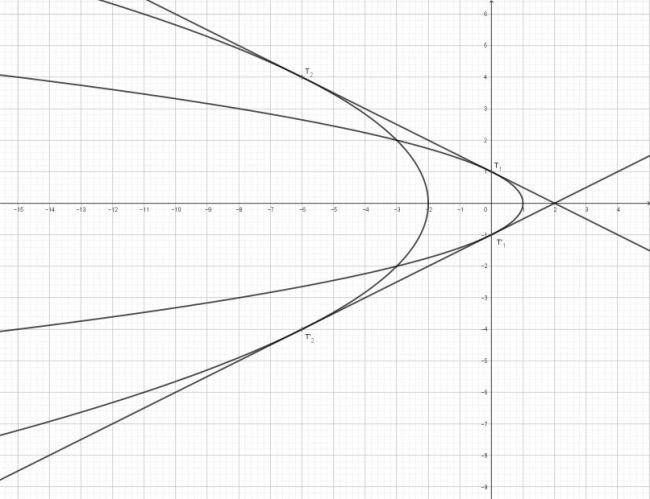
3, Rovnice tečen parabooly: forum.matematika.cz/...

Zdravím,

dám sem řešení večer

První parabola:

Za x dosadit 0

y² = 1

y₁ = 1

y₂ = - 1

Jsou dva průsečíky s osou y

P_y1 [0;1]

P_y2 [0;-1]

--

Za y dosadit 0

x = 1

Průsečík s osou x je :

P_x [1;0]

-------------------

Druhá parabola:

Za x dosadit 0

y² = - 8

Není průsečík s osou y

--

Za y dosadit 0

0 = - 4 . (x + 2)

Průsečík s osou x je :

P_x [- 2;0]

2)

Průsečíky parabol:

Dát rovno:

1 - x = -4 (x + 2)

1 - x = -4x - 8

3x = - 9

x = - 3

Po dosazení do rovnic parabol:

y² = 4

y₁ = 2

y₂ = - 2

P₁ [-3; 2]

P₂ [-3; -2]

K 4)

Tady je odkaz na soubor, kde jsou uvedeny "tvary"parabol

spskarvina.cz/...

k 3)

Možná to lze spočítat takto:

Obecně, rovnice tečny je :

y = kx + q

Místo y do obou dovnic dosadit kx + q

(kx + q)² = 1 - x

k². x² + 2 . k . q . x + q² = 1 - x

k². x² + 2 . k . q . x + x + q² - 1 = 0

--

(kx + q)² = - 4 . (x + 2)

k². x² + 2 . k . q . x + q² = - 4x - 8

k². x² + 2 . k . q . x + 4x + q² + 8 = 0

Diskriminant kvadratické rovnice je obecně:

D = b² - 4 . a . c

Diskriminant první rovnice je:

(2 . k . q + 1)² - 4 . k² . (q² - 1)

Diskriminant druhé rovnice je:

(2 . k . q + 4)² - 4 . k² . (q² + 8)

Protože daná přímky jsou tečny, tak D = 0

(2 . k . q + 1)² - 4 . k² . (q² - 1) = (2 . k . q + 4)² - 4 . k² . (q² + 8)

4 . k . q + 1 + 4 . k² = 16 . k . q + 16 - 32 . k²

36 . k ² - 12 . k . q - 15 = 0

12 . k ² - 4 . k . q - 5 = 0

ZNOVA:

Diskriminant první rovnice je:

(2 . k . q + 1)² - 4 . k² . (q² - 1)

Diskriminant druhé rovnice je:

(2 . k . q + 4)² - 4 . k² . (q² + 8)

Protože dané přímky jsou tečny, tak D = 0

---

(2 . k . q + 1)² - 4 . k² . (q² - 1) = 0

4kq + 1 + 4k² = 0

4k² = - 4kq - 1

(2 . k . q + 4)² - 4 . k² . (q² + 8)

16kq + 16 - 32 k² = 0

--

16kq + 16 - 8 . ( - 4kq - 1 ) = 0

48 kq = - 8

kq = - 1/6

--

12 . k ² - 4 . k . q - 5 = 0

12 . k ² - 4 . (-1/6) - 5 = 0

12 . k ² + 4/6 - 5 = 0

12 . k ² = 26/6

k = odmocnina z 26/72

Sice mám nějaký výsledek, ale nevypadá to jako správný výsledek.

TAKTO JE TO SPRÁVNĚ:

3)

Obecně, rovnice tečny je :

y = kx + q

Místo y do obou dovnic dosadit kx + q

(kx + q)² = 1 - x

k². x² + 2 . k . q . x + q² = 1 - x

k². x² + 2 . k . q . x + x + q² - 1 = 0

--

(kx + q)² = - 4 . (x + 2)

k². x² + 2 . k . q . x + q² = - 4x - 8

k². x² + 2 . k . q . x + 4x + q² + 8 = 0

Diskriminant kvadratické rovnice je obecně:

D = b² - 4 . a . c

Diskriminant první rovnice je:

(2 . k . q + 1)² - 4 . k² . (q² - 1)

Diskriminant druhé rovnice je:

(2 . k . q + 4)² - 4 . k² . (q² + 8)

Protože daná přímky jsou tečny, tak D = 0

(2 . k . q + 1)² - 4 . k² . (q² - 1) = 0

4k²q² + 4kq + 1 - 4k²q² + 4k² = 0

4kq + 1 + 4k² = 0

(2 . k . q + 4)² - 4 . k² . (q² + 8) = 0

4k²q² + 16kq + 16 - 4k²q² - 32k² = 0

16kq + 16 - 32k² = 0

-----

4kq + 1 + 4k² = 0 / krát (-4)

- 16kq - 4 - 16k² = 0

16kq + 16 - 32k² = 0

-------------------------------

po sečtení rovnic vznikne rovnice:

12 - 48 k² = 0

48 k² = 12

k² = 1/4

k₁ = 1/2

k₂ = - 1/2

-------------

Dosadit za k

- 16kq - 4 - 16k² = 0

8q₂ - 4 - 4 = 0

8q₂ = 8

q₂ = 1

Stejně spočítat q₁