Dobrý den,
můžete mi někdo pomoct pochopit následující příklad? Byl jsem dlouhodobě nemocný a ted doháním školu...
Díky moc
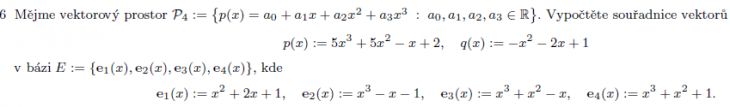
0x
Už jdu spát, takže něco napíšu zítra (vlastně už dnes) odpoledne. Nicméně, mohl byste zatím upřesnit (pokud je to ve vašich silách), co na tom nejvíc nechápete? Není to nutné, je mi jasné, že kdybyste to mohl upřesnit více, už byste byl na půli cesty k pochoopení, ale možná aspoň napsat, co o vektorových prostorech a bázích víte, abychom věděli, čím začít.
0x
Tak nejprve zopakujme základní pojmy, tedy alespoň stručně.
Co je vektor a vektorový prostor? Původně tento pojem pochází z fyziky, kde se tímto pojmem označuje veličina, která má velikost a směr, například síla nebo rychlost a jiné; znázorňuje se orientovanou úsečkou, jejíž velikost vyjadřuje (ve zvoleném měřítku) velikost této veličiny a zaměření (směr) této úsečky samozřejmě charakterizuje směr příslušné fyzikální veličiny. (Samo slovo vektor pochází z latiny a znamená ten, který nese.) No a síly umí fyzika sčítat (skládat) a násobit číslem, a tyto operace splňují určité základní zákony (komutativita, asociativita atd.)
Matematika tento pojem zobecnila: vektorový prostor je každá taková množina, jejíž prvky (nazývané vektory) umíme sčítat a násobit číslem po vzoru skládání sil, a tyto operace splňují výše zmíněné zákony (podrobnosti jste si určitě říkali, nejdete je třeba i na Wikipedii: cs.wikipedia.org/... případně z trochu jiného pohledu cs.wikipedia.org/... a jinde).
Vektorový prostor může být výše zmíněná množina sil (fyzikální vektory), množina orientovaných úseček (tzv. geometrické vektory, které vlastně představují geometrický model, geometrické znázornění fyzikálních vektorů), ale i jiné množiny. Ve vašem příkladě pracujete s vektorovým prostorem všech polynomů stupně nejvýše třetího. Jeho prvky, vektory, jsou tedy polynomy, které umíme sčítat (například (3x + 5) + (4x³ -2) = 4x³ + 3x + 3) a násobit . (Polynomy umíme taky násobit mezi sebou, ale to je vlastnost, která nás z hlediska polynomů jakožto vektorového prostoru nezajímá, tak na ni pro tuto úlohu zapomeňte.)
Prozatím takhle, promyslete si to a já zatím do doplnění otázky napíšu něco o bázích a souřadnicích.
doplněno 17.12.10 14:00:Když už je to v rubrice "cizí jazyky", doplním poznámku ke slovu vektor:
Etymologie _ vysvětlení původu slova:
lat. veho, vectum vézt
Doplnění k pojmům "báze"a "souřadnice vektorů".:
Ve vektorových prostorech konečné dimenze (co to je, to v tomto okamžiku není důležité) existují tzv. BAZE, takové skupiny vektorů, že každý vektor z vektorového prostoru V lze napsat právě jedním způsobem jako součet násobků vektorů báze. Tedy například: ve vektorovém prostoru V (dimenze 3) existují skupiny tří vektorů, například e1, e2 e3, takové že libovolný vektor v z V lze právě jedním způsobem napsat ve tvaru v = v1 *e1 + v2*e2 + v3*e3, No a ta čísla v1, v2, v3 se nazývají
souřadnice vektoru v vzhledem k bázi [e1, e2, e3]
Takových bází je nekonečně mnoho, můžete jim také říkat systém souřadný, ale to vás nemusí teď zajímat. Vy pracujete s vektorovým prostorem polynomů stupně nejvýše třetího (to je, na okraj, prostor dimenze 4) a víte ze zadání, že vektory (polynomy)
e1(x) = x² + 2x + 1,
e2(x) = x³ - x - 1
e3(x) = x³ + x² - x
e4(x) = x³ + x² + 1
bázi tvoří, a vaším úkolem je
a) najít čísla a,b, c,d tak že p(x) = a*e1(x) + b*e2(x) + c*e3(x) + d*e4(x)
b) najít čísla e,f,g,h tak, že q(x) = e*e1(x) + f*e2(x) + g*e3(x) + h*e4(x)
kde p, q jsou polynomy ze zadání. Ta čísla pak budou hledané souřadnice.
Pokud jde o pochopení, mělo by to stačit. Výpočet se provádí tak, že tenhle symbolický zápis rozepíšeme s konkrétními číslu ze zadání, upravíme a využijeme toho, že rovnost polynomů znamená rovnost koeficientů, takže dostaneme systém 4 lineárních rovnic pro čtyři neznámé (samozřejmě dvakrát: jednou pro případ a), podruhé pro případ b).
Pokud budou další problémy, napište.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.