2x
Zdravím,
tady je odkaz na soubor, kde na str. 2 je nakreslen rozvinutý plášť kuželu:
Myslím si, že řešení je takto:
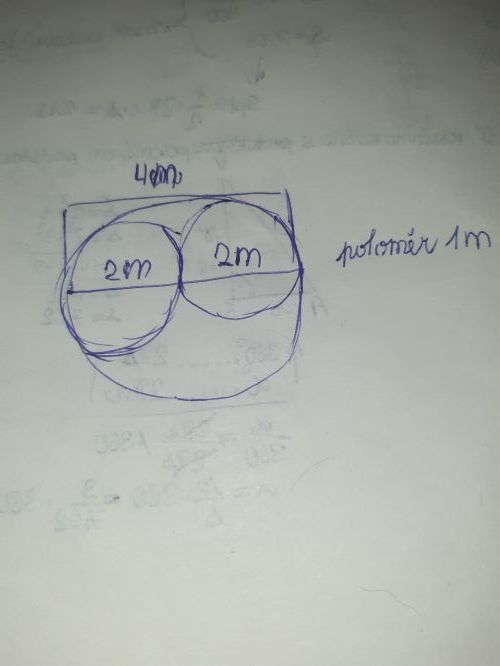
Z daného kruhu byly odříznuty dva pláště bez podstavy. Poloměr toho kruhu je roven délce s "hrany "kuželu.
Průměr kruhu je 4 m, tedy poloměr kruhu je 2 m.
Polovina délky obvodu kruhu folie je rovná celé délce obvodu "hrany"podstavy úkrytu.
Délka obvodu kruhu je :
2 . π . r = 2 . 3,14 . 2 = 12,56 m
Délka obvodu "hrany"podstavy je :
π . r = 3,14 . 2 = 6,28 m
Tedy poloměr "hrany"podstavy ůkrytu je 1 m.
Výšku kuželu spočítáme pythagorovou větou:
12 + v2 = s2
v2 = s2 - 12
v2 = 22 - 12
v = odmocnina ze 3
2x
Měli jednu plachtu o průměru 4 metry a z ní udělali dva stany. Tudíž ji museli rozpůlit. A z každé půlky udělali jeden stan. Půlkruh stočili do kužele. A ten kužel má stranovou výšku půlku průměru plachty. Tedy dva metry. A obvod základny onoho kužele je polovina obvodu celé plachty.
2x
Zdravím. Pokud z kruhu o průměru 4 metry (poloměr 2 m) zhotovili dva shodné kuželové úkryty (úkryt je zřejmě tvořen pláštěm kužele – Spl=π*r*s, jehož strana měří ty 2 metry), je pláštěm kužele polovina kruhu o poloměru 2 m a to je (π*22)/2, což je 2*π a to se rovná plášti, což je π*r*2, neboli 2*π = π*r*2, z toho r=1 (metr). Polovina osového řezu pláště tohoto kužele je pravoúhlý trojúhelník s přeponou 2 m (strana kužele) a odvěsnou 1 m (poloměr podstavy kužele). Hledaná výška kužele je druhou odvěsnou tohoto trojúhelníka. Pythagorova věta: v2=22-12 atd.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.