Dobrý den,
potřebuji nutně pordit s touto úlohou. Nevím si s ní rady. Narýsujte graf závislosti teploty na čase pro ohříváni ztuhlé rtuti z počáteční teploty –45°C na výslednou teplotu
60°C. Teplota tání rtuti je –40°C, teplota varu je rtuti je 357°C. Děkuji předem za odpověd. Petrželová.
5x
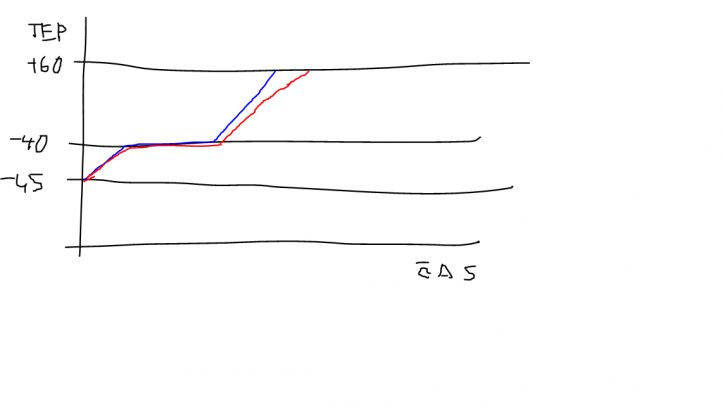
Graf znazornuje dva prubehy.
Modry je idealizovany, linearni, kdy se poicta s tzv. stredni mernou tepelnou kapacitou, cerveny je realny, kdy merna tepelna kapacita s rostouci teplotou roste, tedy cas pro ohrati stejneho objemu se postupne zpomaluje.
Nutnym predpokladem pro kterykoliv z techto prubehu, ktery ze zadani explicitne neplyne, je, ze mnozstvi dodavaneho tepla je konstantni. Tedy se v prubehu casu nemeni!
1. usek znaci ohrev tuheho kovu na teplotu tani
2. usek znaci tani pri konstantni teplote
3. usek znaci ohrev tekuteho kovu na vyslednou teplotu.
2x
Dobrý den,
na vodorovné ose bude čas, na svislé ose teplota. Na vodorovné ose zvolíme (*) časy:
0 - doba, kdy má rtuť teplotu –45 °C,
t1 - doba začátku tání rtuti (–40 °C),
t2 - doba konce tání (opět –40 °C),
t3 - doba, kdy se rtuť ohřála na +60 °C.
Jednotlivé body spojíme úsečkami.
V době od 0 (sekund, minut, ...) do t1 teplota ztuhlé rtuti stoupá, v době od t1 do t2 je úsečka vodorovná - rtuť taje, její teplota v průběhu tání zůstává stálá. Potom teplota opět roste.
(*) Otázka je, jak zvolit časy t1, t2, t3. Není-li zadáno, že rtuť přijímá za stejný čas stejné teplo, můžeme je zvolit libovolně. Přijímá-li rtuť teplo rovnoměrně, budeme muset počítat...
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.