Jehlan obsah

Zdravím. Pro výpočet obsahu trojúhelníkových stěn jehlanu lze použít Heronův vzorec:

Jsou-li a, b, c délky stran trojúhelníku, platí pro jeho obsah:

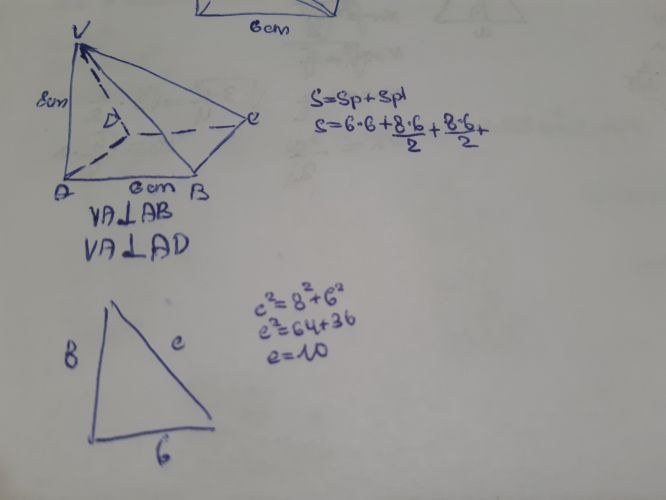
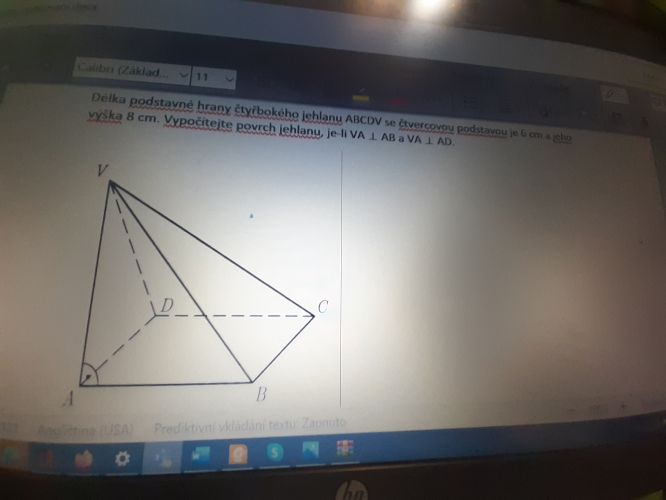
S= druhá odmocnina z výrazu s(s−a)(s−b)(s−c), kde s=(a+b+c )/2 je poloviční obvod trojúhelníku. Je ale třeba znát všechny tři strany trojúhelníka: Trojúhelník DCV: strana DC= 6, strana VD= 8 a stranu VC spočítat Pythagorovou větou jako přeponu trojúhelníka VAC (má u vrcholu A pravý úhel), jehož odvěsny jsou : VA= 8 a AC je úhlopříčka čtverce o straně 6; trojúhelník BCV má stejné strany jako trojúhelník DCV, proto má i stejný obsah....

Zdravím. Jsem se "upsal": Hrana VD není 8, ale 10. Trojúhelník VCD je pravoúhlý (pro jeho strany 6; 10 a √136 platí Pythagorova věta) a oba trojúhelníky (VCD a VCB) mají stejný obsah. Všechny čtyři trojúhelníky, které tvoří plášť tohoto jehlanu jsou pravoúhlé, takže opravdu (jak tady zaznělo) stačí Pythagorova věta...

Vsimnite si na tej fotke, co je kolme : VA je kolme na AB a VA je kolme na AD. Cize to nie je typicky ihlan, kde vrchol je pri pohlade zhora v strede stvorca. Tu je vrchol pri pohlade zhora nad vrchol podstavy A.

Cize trojuholniky VAB a VAD su pravouhle, pravy uhol je vrchole A. Cize plocha VAB a VAD je jasna : 1/2 sucinu hrany podstavy a vysky.

Dalej : BCV je tiez pravouhly, pravy uhol je pri vrchole B, tiez DCV, pravy uhol je pri D. Cisto pyth vetu staci pouzivat.

Myslím si, že ta zadaná výška 8 cm není délka hrany AV

Tak čtu to zadání znova. Ten náčtrt v zadání je nakreslenej chybně. Dle zadání je ten jehlan jakoby "ořízlej" kvádr.

Trojúhelník VAC je na základě zadání taky pravoúhlý trpjúhelník.

Délka AC je 6 . odmocnina ze 2

Asi to nelze spočítat jinak, než heronovým vzorcem.