Nejste přihlášen/a.
2x
Dobrý den, viz např. kapitoly
Graf funkce I, II, Rostoucí a klesající funkce I, II: realisticky.cz/...
Definiční obor se určuje na ose x ("promítneme"si graf svisle dolů či nahoru na osu x), neboli zjistíme, pro která x je funkce definovaná (zadaná). Obor hodnot se určuje na ose y, tj. kterých hodnot může funkce nabývat.
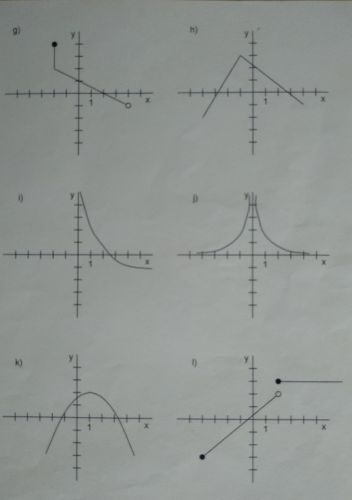
Např. h) def. obor D(f) = (–nekonečno, +nekonečno), obor hodnot H(f) = (–nekonečno; +3]. Místo hranaté závorky se používá zobatá.
2x
Monotonie funkce je možná dobře vysvětlená ve videu, na které dávám odkaz:
Tady je odkaz na soubor, kde je uvedeno, jak zapisovat intervaly
---
Nějaká část grafu funkce je monotonní v případě, když:
např. pravítko (nebo tužka) přiložené k vodorovné ose (rovnoběžně s touto osou) je posouváno tak, aby bylo stále rovnoběžně s vodorovnou osou, tak v dané monotonni části grafu protína tu část grafupři jakémkoliv posunutí jen v jednom bodě.
Monotonní je jenom celý graf funkce i)
Graf funkce i) je na celém intervalu klesající.
----
g) není graf funkce, protože část toho grafu je "čára"kolmo k vodorovné ose
-----
Část grafu funkce h) je rostoucí , na intervalu (- nekonečno, - 1)
Část grafu funkce h) je klesající, na intervalu (- 1, nekonečno)
--------
Část grafu funkce k) je rostoucí , na intervalu (- nekonečno, 1)
Část grafu funkce k) je klesající , na intervalu ( 1 , nekonečno)
----
Část grafu funkce j) je rostoucí , na intervalu (- nekonečno, 0)
Část grafu funkce j) je klesající , na intervalu ( 0 , nekonečno)
2x
Definiční obor je zapisován D(f)
Obor hodnot je zapisován H(f)
---
Tady jsou odkazy na soubory, kde je uvedeno, jak zapisovat intervaly:
------------
Definiční obor určíme tak, že uděláme kolmice z krajních bodů na vodorovnou osu.
Obor hodnot určíme tak, že uděláme kolmice z krajních bodů na svislou osu.
doplněno 24.03.21 13:51:
g)
Daný graf není graf funkce, takže nelze zapsat ani D(f) ani H(f)
h)
D(f) = R
H(f) = ( - nekonečno, 3>
R je množina všech čísel
i)
D(f) = (0 , nekonečno)
H(f) = (-1 , nekonečno)
j)
D(f) = R ∖ {0}
∖ znamená bez (tedy v tomto příkaldě množinu R kromě 0)
H(f) = (0, nekonečno)
k)
D(f) = R
H(f) = (- nekonečno, 2)
l)
D(f) = <-5 , nekonečno)
H(f) = <-3 ; 2) u {3}
u je značka pro sjednoceno
Tady je odkaz na stránku, kde jsou značky
0x
Zdravím. Z definice funkce: Ke každému prvku x z množiny D je přiřazeno právě jedno reálné číslo y. Z toho důvodu není obrázek g) grafem funkce...
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.