4x
Zdravím. V trojúhelníku ASD výška spuštěná z vrcholu D na protější stranu AS (pata této kolmice leží na prodloužení strany AS za bod A) nechť je x. V trojúhelníku ABC je výška příslušná ke straně AB (spuštěná z vrcholu C) také x. Obsah trojúhelníku ASD je 15: 15 = a*x/2 , z toho x = 30/a; obsah trojúhelníku ABC: 2*a*x/2 = a*x , dosaďme za x výraz 30/a (zjištěný z trojúh. ASD): a*x=a*30/a=30; obsah pravoúhlého trojúhelníku ABC pomocí odvěsen: S=(AC*BC)/2, dosaďme za S vypočtených 30 a za BC daných 5: 30 = AC*5/2, z toho odvěsna AC=12. Takže jedna odvěsna v tomto trojúhelníku je 5 a druhá 12. Přepona pomocí Pythagorovy věty vyjde 13 (cm) a to je průměr kružnice, jejíž délka měla být určena. o = π*d = 3,14*13 atd. (cm)... Pozn.: V obrázku u vrcholu A doplnění, že úhel je pravý, se nezakládá na pravdě...
doplněno 13.03.21 10:11:
Zdravím a ještě doplňuji: Jednodušší postup: Oba trojúhelníky (o kterých "je řeč") mají stejnou výšku a k ní příslušná strana je v pravoúhlém trojúhelníku dvakrát větší než strana v rovnoramenném trojúhelníku, obsah pravoúhlého je tedy dvakrát větší než obsah rovnoramenného trojúhelníka. Takže obsah 30, jedna odvěsna 5, druhá odvěsna vyjde 12 atd.
2x
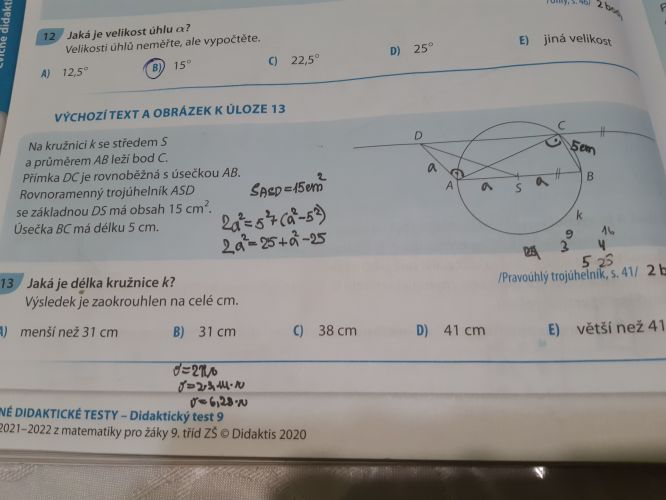
No, vzhldem k tomu, že trojúhelníky ABC a ASD mají stejnou výšku k základně, ležící na průměru AD, tak obsah trojůhelníku ABC je 30cm², a protože úhel ACB je pravý, máme 30=½|AC|*5, odkud vypočteme délku strany BC. (Té vaší rovnici 2a²=5²+(a²-5²) vůbec, ale vůbec nerozumím.) Z Pythagorovy věty můžeme vypočítat průmšěr kružnice k a tedy i její poloměr a, a následně z obsahu trojúhelníka ABC jeho výšku na stranu AB. Tím máme prtakticky všechny údaje, ale... Bod D není tím popisem jednoznačně určen, úhel SAD může být tupý, jak ho máte nakreslen vy, nebo i ostrý, kdy bod D bude uvnitř kružnice k, a vlastně není ani jasně, kde je úhel alfa. Takže po vyjasnění těchto nejednoznačností by to už šlo spočítat.
doplněno 13.03.21 11:59:
Oprava: místo "trojúhelníky ABC a ASD mají stejnou výšku k základně, ležící na průměru AD," má být "trojúhelníky ABC a ASD mají stejnou výšku k základně, ležící na průměru AB" Děkuji @amos ovi za upozornění.
Zdravím a poznamenávám, že pro zjištění požadovaného (délky kružnice) nezáleží na velikosti úhlu u vrcholu A v trojúhelníku ASD, hlavně aby bod D ležel na rovnoběžce s AB vedené bodem C, tedy, aby oba trojúhelníky měly stejnou výšku...
Nejprve ta poslední poznámka: ano, máte samozřejmě pravdu, děkuji. Zkusím to opravit doplněním, když na opravu textu je už pozdě.
No a to ostatní, ano, samozřejmě velikost a a tím i délka kružnice k nezávisí na volně mezi dvěma polohami bodu D, s tím souhlasím. Ale stejně tu ta nejednoznačnost je. A pak otázka, který úhel je ten hledaný alfa.Snad by to měl být úhel CAB, to by odpovídalo klasickému označení úhlů v trojúhelníku ABC, ovšem explicitně to řečeno není a vlastně bych nevylučoval ani to, že jde o úhel DAS a tam užna poloze bodu D záleží. V každém případě bych doplnil tže kjeho výpočtu bych využil goniometrickéfunkce a vhodný pravoúhlý trojúhelník.
Ještě zdravím. Píšete a pátráte po úhlu alfa. Domnívám se, že touto záležitostí se zabývá úloha č. 12, jejíž část je na stejné straně jako úloha č. 13, ale "náš" obrázek s ní nesouvisí...
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.