Nejste přihlášen/a.
0x
Co je vyska vb? Vzdialenost vrcholu B od priamky AC ... cize najdete vzorec na vzdialenost bodu od priamky a dosadite. Napr tu : galeje.sk/...
0x
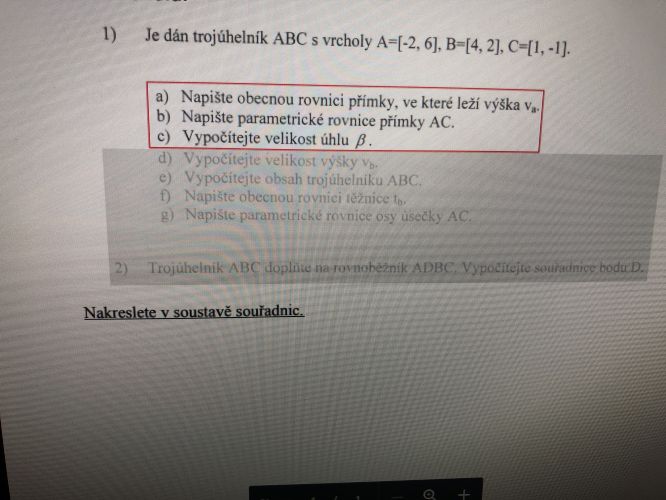
b) Parametrická rovnice přímky má tvar X = A + t.u, kde A je zvolený bod přímky, u je směrový vektor přímky, t je parametr (reálné číslo).
Rozepsáno:
x = a1 + t.u1
y = a2 + t.u2
Za bod A vezmeme bod A[-2,6]. Směrový vektor u=C–A = (3,–7). Tedy
x = –2 + 3t
y = 6 – 7t
Když např. dosadíš t = 0, dostaneš souřadnice bodu A, když dosadíš t = 1, dostaneš souřadnice bodu C, když dosadíš jiné t, dostaneš jiný bod přímky.
0x
a) Výška va je kolmice vedená z bodu A ke straně a = BC.
Rovnici přímky BC najdeme např. ve směrnicovém tvaru y = kx + q. Za x, y dosadíme souřadnice bodu B a C a dostaneme soustavu rovnic:
2 = 4k + q
–1 = k + q
Po výpočtu k, q dostáváme rovnici y = x – 2, obecná rovnice je tedy x – y – 2 = 0.* Normálový (kolmý) vektor této přímky je (1, –1).**
Přímka, v níž leží výška va, je na tuto přímku kolmá. Její normálový (kolmý) vektor dostaneme tak, že u vektoru (1, –1) zaměníme obě složky (–1, 1) a u jedné z nich změníme znaménko, např. (1, 1). Přímka má tedy rovnici x + y + d = 0. Číslo d najdeme tak, že dosadíme rouřadnice bodu A, protože přímka prochází tímto bodem.
* o správnosti se přesvědčíme dosazením souřadnic bodů B, C
** koeficienty u x, y
0x
1a)
Vzorec obecné rovnice přímky je :
ax + by + c = 0
a,b jsou souřadnice normálového vektoru, tedy vektoru kolmého na tuto přímku.
Výška va toho trojúhelníka začíná v bodě A a je kolmá na stranu BC.
Spočítám vektor BC.
1 - 4 je - 3
-1 - 2 je - 3
Vektor BC je (-3;-3)
Nebo lze napsat (3;3)
Tento vektor je kolmý na výšku va , takže je normálovým vektorem .
Obecná rovnice výšky je tedy 3x + 3y + c = 0
Je ještě potřeba dopočítat c.
Za x,y dosadím souřadnice bodu A.
3 krát -2 + 3 krát 6 + c = 0
c = - 12
Výsledek je:
3x + 3y - 12 = 0
0x
1d)
Výška vb je kolmá na stranu AC.
Je potřeba napsat obecnou rovnici strany AC.
Spočítám směrový vektor AC.
1 - (-2) = 3
-1 - 6 = -7
Směrový vektor AC je (3 ; -7)
Normálový vektor je vektor kolmý na AC.
Normálový vektor udělám ze směrového vektoru tak, že prohodím souřadnice a u jedné ze souřadnic změním znaménko.
Normálový vektor je (7 ; 3 )
Obecná rovnice přímky AC je:
7x + 3y + c = 0
Dopočítám c dosazením souřadnic bodu A nebo dosazením souřadnic bodu C . Třeba dosadím souřadnice bodu A.
7 krát (-2) + 3 krát 6 + c = 0
-14 + 18 + c = 0
c = - 4
Obecná rovnice přímky AC je:
7x + 3y - 4 = 0
Spočítám vzdálenost bodu B od této přímky.
Tady je odkaz na soubor, kde je vzorec a postup:
Vzdálenost označím v.
Obecná rovnice přímky AC je 7x + 3y - 4 = 0
7 je jako a
3 je jako b
-4 je jako c
Souřadnice bodu B jsou [4 ; 2]
4 je jako x0 , 2 je jako y0
v = (7 krát 4 + 3 krát 2 - 4) / odmocnina z (72 + 32 )
v = 3,94
Délka vb je 3,94 cm.
doplněno 09.02.21 08:32:
----------------------------------------
1e)
Plocha trojúhelníka je:
S = vb krát /AC/ děleno 2
/AC/ je délka strany AC
Délku strany AC lze spočítat vzorcem pro vzdálenost dvou bodů, tedy je potřeba spočítat vzdálenost bodů A, C.
Tady je odkaz na soubor, kde je postup:
0x
1f)
Je potřeba spočítat střed Sb strany AC.
Tady je odkaz na soubor, kde je na str. 2 vzorec:
Ze souřadnic bodů B a Sb spočítat směrový vektor.
Ze směrového vektoru udělat normálový vektor (a;b) (prohozením souřadnic směrového vektoru a změnou znaménka).
Do obecné rovnice ax + by +c = 0 dosadit souřadnice bodu B (nebo bodu Sb) a dopočítat c.
----------------------
1g)
Spočítat směrový vektor strany AC (tedy z bodů A,C)
Udělat z tohoto směrového vektoru normálový vektor.
Dosadit souřadnice bodu Sb (vypočítané v příkladu 1f) do obecné rovnice a dopočítat c.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.