Dobrý den,
potřeboval bych poradit s tímto příkladem.
Znám výsledek, ale postup výpočtu nikoliv nebo aspoň nevím, jak to přesně spočítat.
Rozdělil jsem faktoriály do n! a dále nevím.
Děkuji za odpověď.
Výsledek je: 1
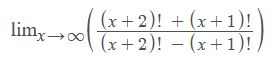
3x
Zdravím. Takže: Čitatel (viz rada od mirek2): (x+1)!*(x+3) ; jmenovatel: (x+2)!-(x+1)!=(x+2)*(x+1)!-(x+1)!=(x+1)!*(x+2-1)=(x+1)!*(x+1) ; čitatele se jmenovatelem vykrátit výrazem (x+1)!, zůstane zlomek (x+3)/(x+1) ; čitatele i jmenovatele vydělit výrazem x, vyjde (1+3/x)/(1+1/x) , tento zlomek "zlimitovat", vyjde (1+0)/(1+0)=1
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.