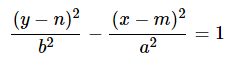Hyperbola - příklad

Číslo –36 převeď na pravou stranu a rovnici vyděl číslem 36. Souřadnice středu a délky poloos získáš porovnáním se středovou rovnicí hyperboly pro tento případ (střed má souřadnice m, n):

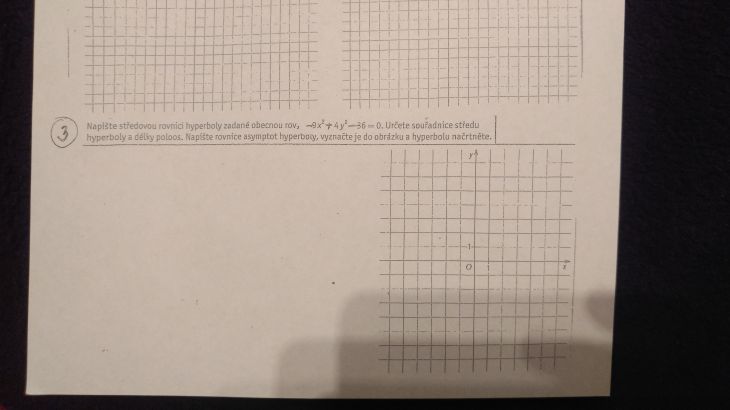
Sředová rovnice bez lineárních členů (x nebo y na prvou) se vypočítá snadno, stačí celou rovnici vydělit číslem odpovídající absolutnímu členu v rovnici hyperboly. Např. rovnici "9x² - 16y² - 225 = 0"číslem 255, rovnici "2x² - 4y² - 16 = 0"číslem 16, ... V tomhle případě 36. Druhý krok je jen tu jedničku přesunou na druhou stranu.

Jakmile získáte středovou rovnici, lehce z toho vyčtete polososy "a"a "b". Rovnici výpočtu asymptot naleznete zde: onlineschool.cz/....

Souřadnice středu ani nemusíte počítat, neboť rovnice neobsahuje lineární členy, takže to je jasné: [0,0]

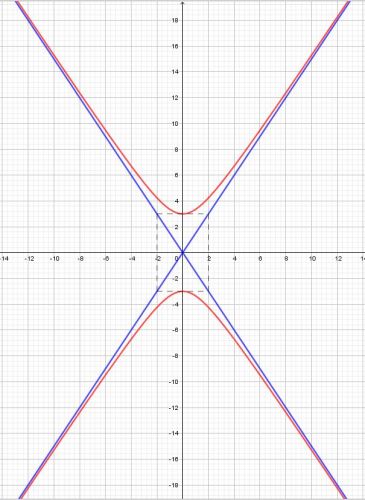
Obrázek snad zvládnete, stačí si vyjádřit y=√(9+...) a dosazovat za "x".

Střed hyperboly tedy leží v počátku: [m, n] = [0, 0].

Vrcholy hyperboly leží na hlavní ose - ta v tomto případě leží na ose y, protože plus je u členu s y².

Protože střed je v počátku, jedna asymptota má rovnici y = (b/a)*x, druhá y = –(b/a)*x.

Viz např. matematika.cz/...

Vrcholy hyperboly lze určit i tak, že najdeme průsečíky s osami. Když zvolíme x = 0, dostaneme y² = 9, což má řešení y = +3, y = –3. a vrcholy mají souřadnice [0, +3] a [0, –3].

Když zvolíme y = 0, dostaneme x² = –4, což nemá řešení, tj. hyperbola nemá průsečíky s osou x.