Prosím zdržte se připomínek, opravdu si nevím rady, předem děkuji za odpovědi.
2x
1. Obrázek, viz wolframalpha.com/...
Pro úhel vektorů platí vzorec dole
doplněno 15.01.21 11:59:
Např. vektor c = AB = B – A = (8 – 3, –2 – 6) = (5, –8).
Velikost vektoru c určíme ze vztahu c2 = 52 + (–8)2.
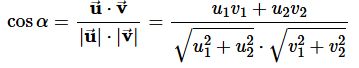
0x
Pri trojuholniku z bodov urobit vektory pre jednotlive strany, potom pouzit vzorec pre odchylku vektorov odtialto: galeje.sk/...
0x
2. Průsečík přímek dostaneme řešením soustavy rovnic.
Výsledek: wolframalpha.com/...
Přímky v obecném tvaru
a1 x + b1 y + c = 0
a2 x + b2 y + d = 0
jsou rovnoběžné, když a2 = k.a1 a zároveň b2 = k.b1.
0x
3. Jestli jsem to dobře opsal, je průsečík wolframalpha.com/...
Přímka r má rovnici 2x – 3y – 9 = 0.
Přímka s ní rovnoběžná má rovnici 2x – 3y + c = 0. Za [x, y] dosaď průsečík přímek p, q a vypočítáš c.
Přímka k ní kolmá má rovnici 3x + 2y + d = 0. Za [x, y] dosaď průsečík přímek p, q a vypočítáš d.
Kolmou přímku k dané přímce dostaneme tak, že zaměníme koeficienty u x, y a u jednoho z nich změníme znaménko. Tak se určuje kolmý vektor, např. k vektoru (2, –3) je kolmý vektor (3, 2).
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.
