Děkuji!
2x
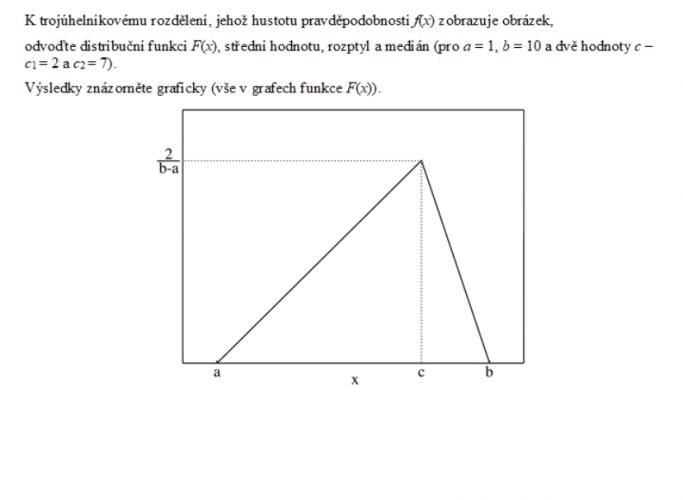
Zdravím, nejdřív je potřeba zjistit rovnice těch dvou přímek. Směrnicová rovnice přímky je y = kx + q. První přímka prochází body [a, 0] a [c, 2/(b-a)], dosadíme je za x, y do rovnice přímky a ze soustavy rovnic určíme k, q. Podobně druhou přímku.
Tím získáš zápis funkce f(x) pro a < x < c (z první přímky) a pro c < x < b (z druhé přímky).
Distribuční funkce F(x) je integrálem f(x), který se spočítá zvlášť pro obě části (první má meze a, c).
Střední hodnotu a rozptyl vypočteš podle vzorců, např. střední hodnota pro spojité rozdělení: cs.wikipedia.org/...
Výsledky by měly vypadat asi takto: cs.wikipedia.org/...
2x
Konkrétně pro a=1, b=10, c=7, tedy 2/(b-a)=2/9. První přímka y=kx+q prochází body [x,y]=[1,0] a [7,2/9]. Po dosazení do rovnice přímky máme 0=k+q a dále 2/9=7k+q. Řešením soustavy rovnic je (jestli dobře počítám) k=1/18, q=–1/18, tedy rovnice přímky je y=x/18 – 1/18 čili y=(x–1)/18.
Tedy v daném intervalu je f(x)=(x–1)/18. O správnosti se můžeme přesvědčit dosazením do cs.wikipedia.org/...
Distribuční funkce v tomto intervalu vypočteme jako integrál (asi bych to počítal obecně, tj. s písmeny a, b, c, d)
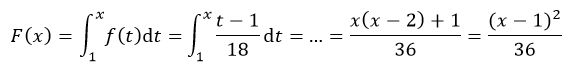
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.