Dobrý den, prosím věděl by někdo jak vyřešit tyto dvě limiy
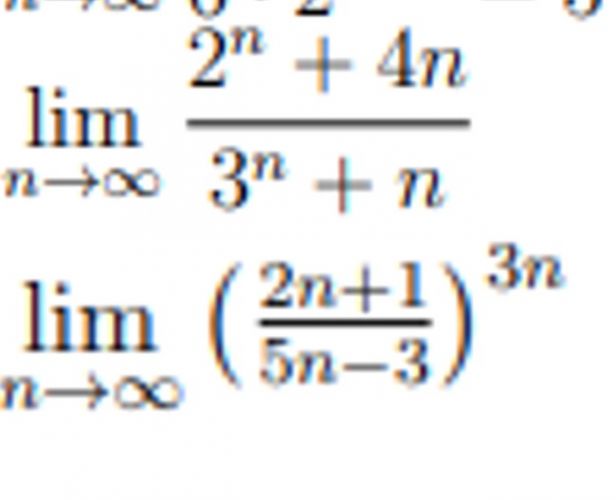
2x
Spodní limitu lze řešit na základě věty, že limita součinu je rovna součinu jednotlivých limit, viz. např. text na stránce, na kterou je tento odkaz
----------------------
[(2n+1)/(5n-3)] umocněno na 3n = [(2n+1)/(5n-3)] krát [(2n+1)/(5n-3)] krát [(2n+1)/(5n-3)] krát ...
protože n je celé kladné číslo
---
lim n se blíží nekonečnu [(2n+1)/(5n-3)] = 2/5
Je to podíl koeficientů před n
---
lim n se blíží nekonečnu [2/5] umocněno na 3n = 0
Tedy výsledek spodní limity je 0.
2x
Tak v prvním příkladu je oprzavdu nejjednodušší vytknut z čitatele 2n a ze jmenovatele 3n. Tím dostaneme před zbytek výrazu mocninu (2/3)n, což konverguje k nule, a to bude násobeno zlomkem, v jehož čitateli je výraz 1+(4n)/(2n), který konverguje k jedné, a podobně jmenovatel bude mít též za limitu jedna.Čili celý výraz konverguje k nule. Q.E.D.
doplněno 31.12.20 12:16:
Když jsem se teď podíval na Lopezzův postup, zdá se mi, že dělá v podstatě totéž, jen zbytečně komplikovaně. A já se ještě jednou omlouvám, původně jsem si to představoval zpaměti koukaje na mobil, a pozdněnoční bludná úvaha mi vnukla nesmyslnou představu o limitě toho vytčeného zlomku.
1x
První limitu lze možná spočítat takto:
Čitatel zlomku i jmenovatel zlomku vydělit n.
(2n /n + 4) / (3n /n + 1) = (2n /n ) / (3n /n + 1) + 4 / (3n /n + 1)
Lze použít větu, že limita součtu funkcí je rovna součtu limit jednotlivých funkcí.
lim 4 / (3n /n + 1) = 0, protože lim 3n /n je nekonečno
---
(2n /n ) / (3n /n + 1) = (2n) / (3n + n)
Protože (2n) / (3n + n) < (2n) / (3n )
tak lim (2n) / (3n ) > lim (2n) / (3n + n)
lim (2n) / (3n ) = lim (2/3)n = 0
(protože to píšu na klávesnici tak jsem za lim nenapsal, že se blíží k nekonečnu, aby to bylo přehlednější)
Tedy výsledek příkladu je 0.
0x
Zdravím, na první limitu bych použil l´Hospitalovo pravidlo, v druhé limitě vytkni n v čitateli i ve jmenovateli.
Návody na řešení rozmanitých limit: math.feld.cvut.cz/...
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.