Nejste přihlášen/a.
Prosim pomozte mi nemohu vyresit.
Na zahradě stály tři bedny s jablky. Celkem bylo jablek více než 150, avšak méně než 190. Maruška přemístila z první bedny do dvou dalších beden jablka tak, že se jejich počet v každé z těchto dvou beden oproti předchozímu stavu zdvojnásobil. Obdobným způsobem Marta přemístila jablka z druhé bedny do první a třetí. Nakonec Šárka podle stejných pravidel přemístila jablka z třetí bedny do první a druhé. Když přišel na zahradu Vojta, podivil se, že v každé bedně byl stejný počet jablek. Kolik jablek bylo v jednotlivých bednách původně?
dekkuji
3x
Zdravím.
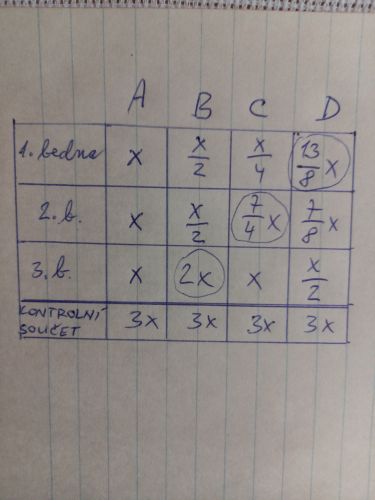
Původně jsem neměl v úmyslu sem "dávat" řešení této úlohy (když je soutěžní), ale abych obhájil "řešení odzadu" proti názoru, že jde o "pokus omyl", uvádím: Vysvětlivky k níže uvedené tabulce: x – počet jablek na konci, sloupec A – stav v bednách na konci přemisťování (po přemístění z třetí bedny...), sloupec B – stav v bednách po přemístění z druhé bedny, sloupec C – stav po přemístění z první bedny, sloupec D – stav na začátku. Vzhledem k sloupci D musí být x dělitelné osmi a celkové množství 3x musí být dělitelné třemi, tedy 3x musí být dělitelné třemi i osmi (nebo číslem 24). V daném rozmezí počtu jablek 150 – 190 vyhovuje této podmínce pouze číslo 168 – takže jediné řešení 3x = 168; x = 56. V každé bedně bylo na konci 56 jablek, původní stav jsou počty 91, 49, 28...
Dobrý den,
mohla bych poprosit o lepsi vysvětlení, konkrétně teda sloupce C,D? Jak jste se dostal z x/2 na 7/4x nebo z x/4 ke 18/8x?
dekuji
Zdravím a pokusím se.
Viz tabulka:
Jak v druhé bedně z x/2 na (7/4)x: Bere se z druhé bedny: Má-li přerozdělením v 1.bedně (kde je x/4) vzniknout dvojnásobek (tedy x/2), je třeba přendat z 2. bedny do 1. bedny x/4. Má-li v 3. bedně (kde je x) vzniknout dvojnásobek (tedy 2x), je třeba přendat x, tedy\ celkem přesunout x+x/4=(5/4)x a protože je třeba, aby v 2. bedně zbylo x/2, musí tam před tímto přerozdělením být (5/4)x+x/2=(7/4)x!
Jak v první bedně z x/4 na (13/8)x – ne na 18/8 jak je psáno v dodatečném dotazu!:Bere se z 1. bedny: Má-li v 2.bedně vzniknout zdvojnásobením (7/4)x, musíme k původním (7/8)x přidat (7/8)x. Má-li v 3.bedně vzniknout zdvojnásobením x, musíme k x/2 přidat x/2 a protože je třeba , aby v 1. bedně zbylo po tomto přerozdělení x/4, musí tam před tímto přerozdělením být to, co tam zbylo (tedy x/4) plus to, co bylo odebráno (x/2+7x/8) a to je celkem (13/8)x ....
0x
Zdravím.
Dovoluji si tvrdit, že původně byl počet jablek v bednách 91, 49 a 28. Příklad bych řešil "odzadu"... Myslím si, že "pověsit" sem řešení nemá cenu vzhledem k tomu, že jde o soutěžní příklad a nejméně v okresním kole (konaném za dozoru) nebudou rady poradny k dispozici. Neúčastí na MO se jistě svět nezboří...
Moc vám děkuji. Vlastně se mi to minuly rok povedlo umistit se na 3 místo v okresním kole. Ale z touhle úlohou jsem si opravdu nevěděl rady proto jsem se rozhodl napsat do poradny. Nicméně vám moc děkuji. A hlavně dekuju za radu! Takovýhle úlohy budu dělat raději odzadu moc děkuji za postup, protože MATEMATIKA JE O POSTUPU! a nějak se podívám jak jste tuhle úlohu vyresil. Moc vám děkuji!
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.